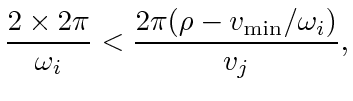Next: Appendix C: Direct cyclic
Up: Rendezvous Without Coordinates1
Previous: Appendix A: Possible Sensor
Appendix B: Remaining Proofs
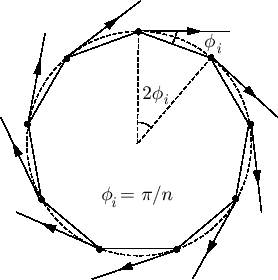
Figure 8:
A regular  -gon with agents on the vertices and moving along the lines tangent to the enclosing circle of the
-gon with agents on the vertices and moving along the lines tangent to the enclosing circle of the  -gon.
-gon.
 |
PROOF OF LEMMA 3. For 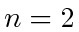 ,
,
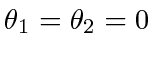 and it is possible that
and it is possible that
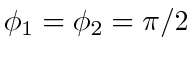 by assumption; substituting these into (9) gives
by assumption; substituting these into (9) gives
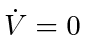 . For
. For 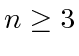 , since agents may take arbitrary initial formation, they may lie exactly on the vertices of a regular polygon and have the agents on the next vertex (say clockwise direction, see Fig. 8) as their targets; all agents can also have
, since agents may take arbitrary initial formation, they may lie exactly on the vertices of a regular polygon and have the agents on the next vertex (say clockwise direction, see Fig. 8) as their targets; all agents can also have
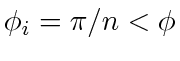 . In this case, since
. In this case, since
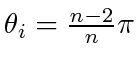 for all
for all  ,
,
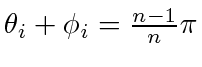 . Substituting these into (9) again gives
. Substituting these into (9) again gives
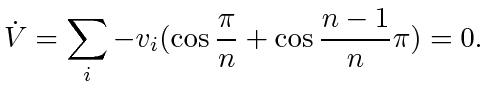 |
(44) |
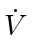 can be easily made strictly positive by letting
can be easily made strictly positive by letting
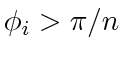 for all
for all  .
.
PROOF OF LEMMA 6. When all
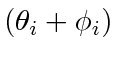 are equal and in the interior of
are equal and in the interior of
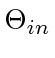 , we have
, we have
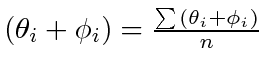 for all
for all  . Hence, at the stationary point,
. Hence, at the stationary point,
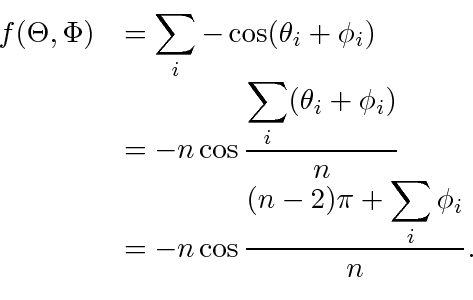 |
(45) |
By (45), this unique stationary point of 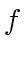 only depends on
only depends on
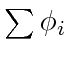 but not on the individual
but not on the individual 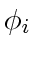 's. Also, fixing
's. Also, fixing 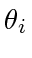 's, the maximum of the last expression in (45) increases as
's, the maximum of the last expression in (45) increases as
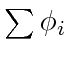 increases; hence, the upper bound of
increases; hence, the upper bound of 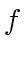 is given by (21).
is given by (21).
PROOF OF LEMMA 7. We may fix 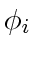 's, in which case
's, in which case
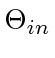 forms a
forms a  -dimensional cube (including the boundary) in the
-dimensional cube (including the boundary) in the  -dimensional Euclidean space with
-dimensional Euclidean space with
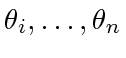 as the coordinates.
as the coordinates.
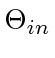 is fully surrounded by
is fully surrounded by
 . Together,
. Together,
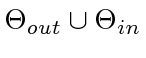 forms a larger
forms a larger  -dimensional cube. Since the
-dimensional cube. Since the 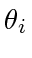 's must also satisfy the constraint
's must also satisfy the constraint
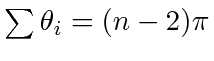 , the valid
, the valid 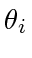 's for simple polygon formation live on the slice of the
's for simple polygon formation live on the slice of the
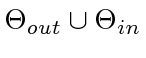 cube cut by the hyperplane
cube cut by the hyperplane
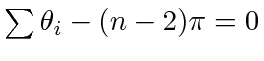 . Geometrically, the slice through
. Geometrically, the slice through
 forms an annulus on the hyperplane
forms an annulus on the hyperplane
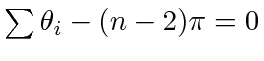 , and the slice through
, and the slice through
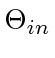 is the inside of that annulus. Fig. 9 illustrates these for the case of
is the inside of that annulus. Fig. 9 illustrates these for the case of 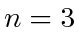 . By continuity of
. By continuity of 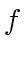 ,
,
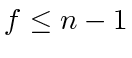 on the boundary of the
on the boundary of the
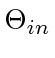 slice since the boundary is the inner part of the closure of the
slice since the boundary is the inner part of the closure of the
 slice. On the other hand, the
slice. On the other hand, the
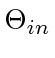 slice is closed and bounded hence compact. By the extreme value theorem,
slice is closed and bounded hence compact. By the extreme value theorem, 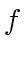 must take both maximum and minimum value on the
must take both maximum and minimum value on the
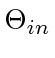 slice. Therefore,
slice. Therefore, 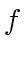 takes value no more than the larger of
takes value no more than the larger of 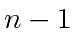 and (21) from Lemma 6.
and (21) from Lemma 6.
Figure 9:
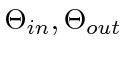 and the slices cut by the
and the slices cut by the
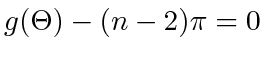 hyperplane, for the case of
hyperplane, for the case of 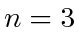 and
and
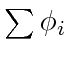
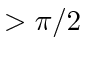 .
.
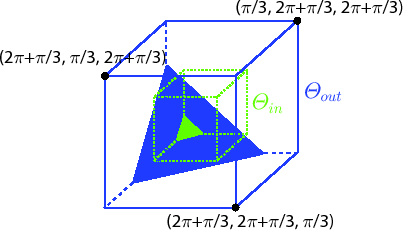 |
Combining the
 and
and
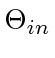 slices, we obtain for any simple
slices, we obtain for any simple  -gon that (22) holds. To ensure
-gon that (22) holds. To ensure
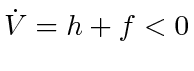 , we need
, we need 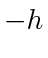 to be more than the right hand side of (22) and rearranging the resulting inequality yields (11). We note that the easily verified fact that for all
to be more than the right hand side of (22) and rearranging the resulting inequality yields (11). We note that the easily verified fact that for all
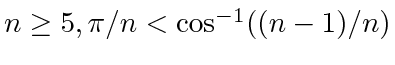 is used.
is used.
Figure 10:
(a) 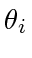 's and
's and
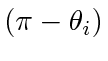 's for a self-intersecting polygon, as marked by the solid arcs and dashed arcs, respectively. The arrow marks the walker's walking direction and starting edge. (b)
's for a self-intersecting polygon, as marked by the solid arcs and dashed arcs, respectively. The arrow marks the walker's walking direction and starting edge. (b) 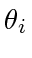 's can be made arbitrarily small by ``pressing'' this polygon from left and right.
's can be made arbitrarily small by ``pressing'' this polygon from left and right.
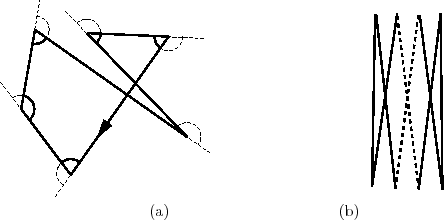 |
PROOF OF LEMMA 8. When the polygon is self-intersecting, the internal angles are no longer well defined; therefore, the constraint, 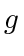 , will change. However, for our purpose of calculating
, will change. However, for our purpose of calculating
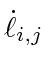 , we can always pick the smaller of the two angles at any vertex of the polygon, since such choice does not affect the value of the cosine function. We define these angles as
, we can always pick the smaller of the two angles at any vertex of the polygon, since such choice does not affect the value of the cosine function. We define these angles as 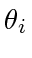 and look at
and look at
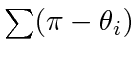 . If we start from any edge of a polygon, self-intersecting or not, and walk along the edges to get back to the starting edge, all the
. If we start from any edge of a polygon, self-intersecting or not, and walk along the edges to get back to the starting edge, all the
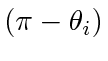 's must add up to at least
's must add up to at least 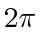 (see Fig. 10(a)). This is true since the walker must turn at least a cycle to get back and
(see Fig. 10(a)). This is true since the walker must turn at least a cycle to get back and
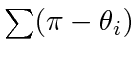 is exactly the sum of the angles turned. Thus
is exactly the sum of the angles turned. Thus
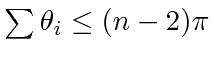 . The constraint function
. The constraint function 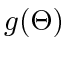 can again be defined as that in (17). For self-intersecting polygon,
can again be defined as that in (17). For self-intersecting polygon, 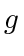 can be arbitrarily close to 0
(see Fig. 10(b)). Therefore,
can be arbitrarily close to 0
(see Fig. 10(b)). Therefore,
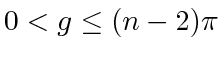 and (20) becomes
and (20) becomes
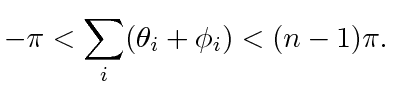 |
(46) |
As stated in Lemma 7, we only need to worry about the part of
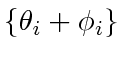 that belongs to
that belongs to
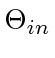 . That is, the interesting
. That is, the interesting 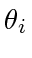 's must comply to
's must comply to
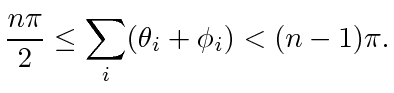 |
(47) |
We may fix 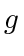 satisfying (47) as a constraint and apply the method of Lagrange multipliers similarly; bounds from Lemma 7 clearly hold.
satisfying (47) as a constraint and apply the method of Lagrange multipliers similarly; bounds from Lemma 7 clearly hold.
Figure 11:
Dubins car agent  that just loses its target
that just loses its target 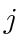 at point
at point 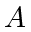 .
.
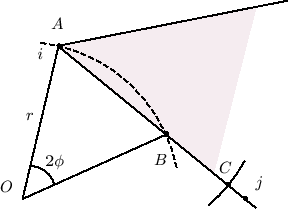 |
PROOF OF PROPOSITION 16. We look at the instant 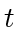 when agent
when agent  just loses sight of agent
just loses sight of agent 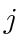 . If agent
. If agent 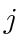 is within distance
is within distance 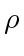 of
of  then they must have merged; suppose not. The setting is shown in Fig. 11: Agent
then they must have merged; suppose not. The setting is shown in Fig. 11: Agent  is initially located at
is initially located at 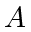 and the ray
and the ray
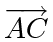 can be imagined as the right boundary of agent
can be imagined as the right boundary of agent  's field of view (shaded area in figure); it cannot see anything to the right of
's field of view (shaded area in figure); it cannot see anything to the right of
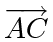 . Let
. Let
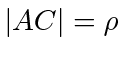 , the merging radius. At that instant, agent
, the merging radius. At that instant, agent  's field-of-view cone is rotating around
's field-of-view cone is rotating around 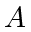 with angular velocity
with angular velocity 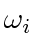 . To stay out of
. To stay out of  's windshield, agent
's windshield, agent 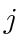 's velocity projection on the direction perpendicular to
's velocity projection on the direction perpendicular to 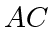 must be greater than
must be greater than
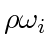 . If
. If
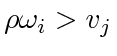 , then once
, then once 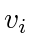 starts to rotate, it will be able to get
starts to rotate, it will be able to get 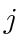 back into its windshield again. This condition is equivalent to (40).
back into its windshield again. This condition is equivalent to (40).
PROOF OF PROPOSITION 17.
Figure 12:
Agent at 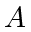 turns along a circle with center
turns along a circle with center 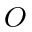 of radius
of radius 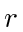 , leaving the small solid circle as its trace. The two large dotted circles are of distance
, leaving the small solid circle as its trace. The two large dotted circles are of distance 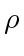 to the agent at
to the agent at 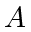 and
and 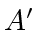 . The shaded disc denotes the intersection of all discs with radius
. The shaded disc denotes the intersection of all discs with radius 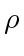 from the agent as it turns a full cycle.
from the agent as it turns a full cycle.
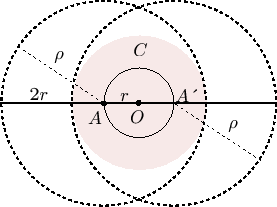 |
First let us assume that  travels at constant speed
travels at constant speed 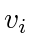 . In Fig. 12, assume that agent
. In Fig. 12, assume that agent  is initially located at
is initially located at 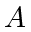 and turns clockwise around
and turns clockwise around 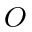 with radius
with radius 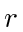 . As it turns around, the intersection of all discs of radius
. As it turns around, the intersection of all discs of radius 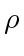 with
with  as the moving center is again a disc (the shaded area
as the moving center is again a disc (the shaded area 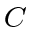 ) of radius
) of radius 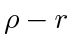 centered at
centered at 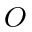 (This can be easily shown: any point inside
(This can be easily shown: any point inside 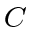 is in all of the moving discs of radius
is in all of the moving discs of radius 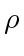 and any point outside
and any point outside 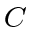 is not in at least one of the moving discs). Since any agent falling into
is not in at least one of the moving discs). Since any agent falling into 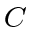 will merge with
will merge with  , to avoid being found by
, to avoid being found by  , an agent, say
, an agent, say 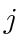 , must move outside
, must move outside 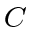 and as
and as  turns two full cycles,
turns two full cycles, 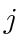 must turn at least one full cycle to avoid appearing in
must turn at least one full cycle to avoid appearing in  's windshield. Hence, if it takes less time for
's windshield. Hence, if it takes less time for  to turn two cycles than for
to turn two cycles than for 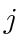 to turn one cycle,
to turn one cycle,
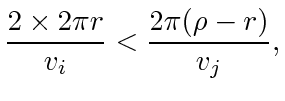 |
(48) |
agent  will then find an existing agent or merge with it. The inequality (48) yields the condition
will then find an existing agent or merge with it. The inequality (48) yields the condition
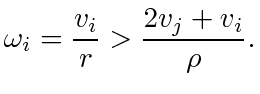 |
(49) |
Selecting (41) is then enough to guarantee that  regains liveness and the system will rendezvous. If
regains liveness and the system will rendezvous. If  is not constant, since
is not constant, since 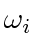 remains a constant by assumption, the intersection must have a minimum radius of
remains a constant by assumption, the intersection must have a minimum radius of
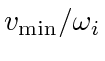 from
from 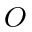 . In this case, we need
. In this case, we need
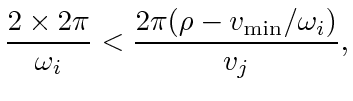 |
(50) |
which is also satisfied by (41). Lastly, (40) from Proposition 16 is also satisfied.



Next: Appendix C: Direct cyclic
Up: Rendezvous Without Coordinates1
Previous: Appendix A: Possible Sensor
Jingjin Yu
2011-01-18


![]() are equal and in the interior of
are equal and in the interior of
![]() , we have
, we have
![]() for all
for all ![]() . Hence, at the stationary point,
. Hence, at the stationary point,
![]() 's, in which case
's, in which case
![]() forms a
forms a ![]() -dimensional cube (including the boundary) in the
-dimensional cube (including the boundary) in the ![]() -dimensional Euclidean space with
-dimensional Euclidean space with
![]() as the coordinates.
as the coordinates.
![]() is fully surrounded by
is fully surrounded by
![]() . Together,
. Together,
![]() forms a larger
forms a larger ![]() -dimensional cube. Since the
-dimensional cube. Since the ![]() 's must also satisfy the constraint
's must also satisfy the constraint
![]() , the valid
, the valid ![]() 's for simple polygon formation live on the slice of the
's for simple polygon formation live on the slice of the
![]() cube cut by the hyperplane
cube cut by the hyperplane
![]() . Geometrically, the slice through
. Geometrically, the slice through
![]() forms an annulus on the hyperplane
forms an annulus on the hyperplane
![]() , and the slice through
, and the slice through
![]() is the inside of that annulus. Fig. 9 illustrates these for the case of
is the inside of that annulus. Fig. 9 illustrates these for the case of ![]() . By continuity of
. By continuity of ![]() ,
,
![]() on the boundary of the
on the boundary of the
![]() slice since the boundary is the inner part of the closure of the
slice since the boundary is the inner part of the closure of the
![]() slice. On the other hand, the
slice. On the other hand, the
![]() slice is closed and bounded hence compact. By the extreme value theorem,
slice is closed and bounded hence compact. By the extreme value theorem, ![]() must take both maximum and minimum value on the
must take both maximum and minimum value on the
![]() slice. Therefore,
slice. Therefore, ![]() takes value no more than the larger of
takes value no more than the larger of ![]() and (21) from Lemma 6.
and (21) from Lemma 6.

![]() , will change. However, for our purpose of calculating
, will change. However, for our purpose of calculating
![]() , we can always pick the smaller of the two angles at any vertex of the polygon, since such choice does not affect the value of the cosine function. We define these angles as
, we can always pick the smaller of the two angles at any vertex of the polygon, since such choice does not affect the value of the cosine function. We define these angles as ![]() and look at
and look at
![]() . If we start from any edge of a polygon, self-intersecting or not, and walk along the edges to get back to the starting edge, all the
. If we start from any edge of a polygon, self-intersecting or not, and walk along the edges to get back to the starting edge, all the
![]() 's must add up to at least
's must add up to at least ![]() (see Fig. 10(a)). This is true since the walker must turn at least a cycle to get back and
(see Fig. 10(a)). This is true since the walker must turn at least a cycle to get back and
![]() is exactly the sum of the angles turned. Thus
is exactly the sum of the angles turned. Thus
![]() . The constraint function
. The constraint function ![]() can again be defined as that in (17). For self-intersecting polygon,
can again be defined as that in (17). For self-intersecting polygon, ![]() can be arbitrarily close to 0
(see Fig. 10(b)). Therefore,
can be arbitrarily close to 0
(see Fig. 10(b)). Therefore,
![]() and (20) becomes
and (20) becomes