To rendezvous, agents must move relative to each other in some way. We formalize this relationship as assignment: we say that agent ![]() is assigned to agent
is assigned to agent ![]() if
if ![]() is
is ![]() 's target. We define the assignment graph
's target. We define the assignment graph ![]() in an obvious way:
in an obvious way: ![]() initially has
initially has ![]() vertices, one for each agent, and there is a directed edge
vertices, one for each agent, and there is a directed edge ![]() from
from ![]() to
to ![]() if and only if agent
if and only if agent ![]() is assigned to agent
is assigned to agent ![]() . The set of edges of
. The set of edges of ![]() is denoted
is denoted ![]() . For an edge
. For an edge ![]() , let
, let
![]() denote the distance between agents
denote the distance between agents ![]() 's positions in
's positions in
![]() . With the introduction of the assignment graph, we define merging properly as: the merging of agent
. With the introduction of the assignment graph, we define merging properly as: the merging of agent ![]() into agent
into agent ![]() is triggered if
is triggered if
We say that an assignment graph ![]() is connected (or weakly connected) if its underlying undirected graph has a single component. We say that
is connected (or weakly connected) if its underlying undirected graph has a single component. We say that ![]() is live if it has at least one edge. If a graph only has a single vertex, we call it live by definition. It is desirable to maintain liveness in
is live if it has at least one edge. If a graph only has a single vertex, we call it live by definition. It is desirable to maintain liveness in ![]() at all times. If
at all times. If ![]() is not live, then it has more than one vertex but no edges; it is then not possible for the system to rendezvous without additional assumptions. Since liveness is not preserved under merging, we need a stronger property from the initial graph. Assuming that an agent never loses its target prior to merging, this property is captured in the following lemma.
is not live, then it has more than one vertex but no edges; it is then not possible for the system to rendezvous without additional assumptions. Since liveness is not preserved under merging, we need a stronger property from the initial graph. Assuming that an agent never loses its target prior to merging, this property is captured in the following lemma.
``Only if" If ![]() is not connected, then it has more than one connected component. By merging we can collapse each connected component to a single point. This results in a graph with more than one vertex and no edges, which is not live.
is not connected, then it has more than one connected component. By merging we can collapse each connected component to a single point. This results in a graph with more than one vertex and no edges, which is not live.
By Lemma 1, for a system of ![]() agents to rendezvous, the assignment graph
agents to rendezvous, the assignment graph ![]() for the system must have at least
for the system must have at least ![]() edges that connect all the vertices. If a connected graph with
edges that connect all the vertices. If a connected graph with ![]() nodes has
nodes has ![]() edges, it is a tree. In particular, in an
edges, it is a tree. In particular, in an ![]() edge connected assignment graph, all vertices but one have a single outgoing edge, making the graph an intree, a directed acyclic graph in which all maximal directed paths point to a single vertex, its root. The agent at the root of the tree has no assigned target; hence, it does not move by the control law.
edge connected assignment graph, all vertices but one have a single outgoing edge, making the graph an intree, a directed acyclic graph in which all maximal directed paths point to a single vertex, its root. The agent at the root of the tree has no assigned target; hence, it does not move by the control law.
 |
The condition to guarantee rendezvous for an intree assignment graph will turn out to be quite trivial. However, such a formation is asymmetric in the sense that exactly one of the agents (the root) has no assignment. Such an assignment is not possible to achieve in a decentralized manner. The simplest symmetrical assignment graph ![]() has
has ![]() assignments, one for each agent. We do not investigate the case in which one agent has more than one assignment at a given instant, since a more complicated control protocol will be required. Let us denote the assignment graph of our interest as single-target assignment graph. When
assignments, one for each agent. We do not investigate the case in which one agent has more than one assignment at a given instant, since a more complicated control protocol will be required. Let us denote the assignment graph of our interest as single-target assignment graph. When ![]() has
has ![]() edges, the extra edge induces a cycle; therefore
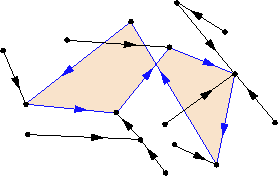
edges, the extra edge induces a cycle; therefore ![]() has a single cycle on which each agent is assigned to the next one. The assignment also guarantees that any agent not on a cycle has a directed path to agents on the cycle (see Fig. 3). The behavior of the agents on the cycle is not affected by any agent not on the cycle. As we shall see later, this observation plays an important role in obtaining sufficient conditions for guaranteed rendezvous.
has a single cycle on which each agent is assigned to the next one. The assignment also guarantees that any agent not on a cycle has a directed path to agents on the cycle (see Fig. 3). The behavior of the agents on the cycle is not affected by any agent not on the cycle. As we shall see later, this observation plays an important role in obtaining sufficient conditions for guaranteed rendezvous.
Given an assignment graph ![]() , we may define a function of the form
, we may define a function of the form
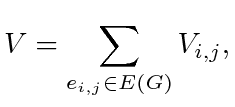 |
(5) |
``Only if" If ![]() is not connected, then it has more than one connected component. If each connected component collapses to a single point,
is not connected, then it has more than one connected component. If each connected component collapses to a single point, ![]() becomes zero, even though we do not have rendezvous of all agents.
As an alternative to the above direct proof, we could deduce Lemma 2 from Lemma 1: by liveness, the graph will have at least one edge (and thus
becomes zero, even though we do not have rendezvous of all agents.
As an alternative to the above direct proof, we could deduce Lemma 2 from Lemma 1: by liveness, the graph will have at least one edge (and thus ![]() will be positive) as long as rendezvous does not occur.
will be positive) as long as rendezvous does not occur.