


Next: The cyclic case
Up: Guaranteed Rendezvous of Identical
Previous: Guaranteed Rendezvous of Identical
Based on an assignment graph 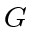 , we define a candidate Lyapunov function
, we define a candidate Lyapunov function
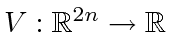 as
as
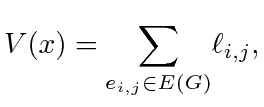 |
(6) |
This definition of 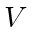 is insensitive to edge directions in
is insensitive to edge directions in 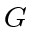 . Unlike more conventional quadratic Lyapunov functions, this specific
. Unlike more conventional quadratic Lyapunov functions, this specific 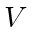 takes a form linear in
takes a form linear in
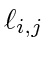 , which means that the corresponding time derivative is not linear in
, which means that the corresponding time derivative is not linear in
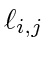 or
or 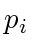 . The reason for the choice of the Lyapunov function will become clear in the next subsection. When a merge happens, we assume that the distance between the two merged agents is frozen, which is achievable by synchronizing their control. This gives us a continuous
. The reason for the choice of the Lyapunov function will become clear in the next subsection. When a merge happens, we assume that the distance between the two merged agents is frozen, which is achievable by synchronizing their control. This gives us a continuous 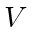 . Alternatively, we could also let the two merged agents have zero distance, which would induce a jump in
. Alternatively, we could also let the two merged agents have zero distance, which would induce a jump in 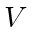 . Since a system with
. Since a system with  agents only has up to
agents only has up to 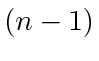 merges, these discontinuities would not affect the overall rendezvous behavior of the system.
merges, these discontinuities would not affect the overall rendezvous behavior of the system.
The function 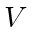 defined in (6) is clearly a graph-compatible Lyapunov function. By Lemma 2, it is rendezvous positive definite if and only if
defined in (6) is clearly a graph-compatible Lyapunov function. By Lemma 2, it is rendezvous positive definite if and only if 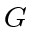 is connected. We may then study the behavior of this Lyapunov function over single-target assignment graphs to derive sufficent conditions for rendezvous of the system. For moving agents,
is connected. We may then study the behavior of this Lyapunov function over single-target assignment graphs to derive sufficent conditions for rendezvous of the system. For moving agents, 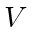 can be considered as a function of time; its time derivative is then
can be considered as a function of time; its time derivative is then
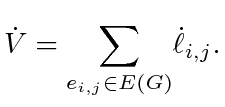 |
(7) |



Next: The cyclic case
Up: Guaranteed Rendezvous of Identical
Previous: Guaranteed Rendezvous of Identical
Jingjin Yu
2011-01-18
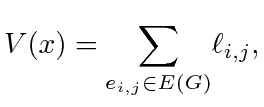
![]() defined in (6) is clearly a graph-compatible Lyapunov function. By Lemma 2, it is rendezvous positive definite if and only if
defined in (6) is clearly a graph-compatible Lyapunov function. By Lemma 2, it is rendezvous positive definite if and only if ![]() is connected. We may then study the behavior of this Lyapunov function over single-target assignment graphs to derive sufficent conditions for rendezvous of the system. For moving agents,
is connected. We may then study the behavior of this Lyapunov function over single-target assignment graphs to derive sufficent conditions for rendezvous of the system. For moving agents, ![]() can be considered as a function of time; its time derivative is then
can be considered as a function of time; its time derivative is then