Planning and Learning Techniques for Very Large Markov Decision Processes

Mobile Autonomous Robotics (MARS) Project

Terran Lane, Postdoctoral Researcher, LIS Group

Introduction

While Markov Decision Processes (MDPs) are quite general and expressive models for reasoning about actions in the face of uncertainty, they don't scale well to the very large state spaces in which we're really interested. In particular, while exact reasoning algorithms for MDPs run in time polynomial in the size of the total state space, many problems of interest to AI researchers are best written in terms of discrete state variables. The total state space, then, is the cross product of the individual variables and reasoning methods are then exponential in the number of state variables. For example, we are currently working with a model of a package delivery problem that has a total state space of roughly 2500 states.

A number of decomposition, abstraction, and approximation techniques to address this exponential complexity have been proposed by various researchers. (A brief and far from complete bibliography of related papers on the subject can be found here.) Our current belief is that a true solution to this problem will involve parts of many of these proposals (or, ideally, an as yet unconceived generalization that encompasses all of these ideas). We are particularly interested in examining ideas based on

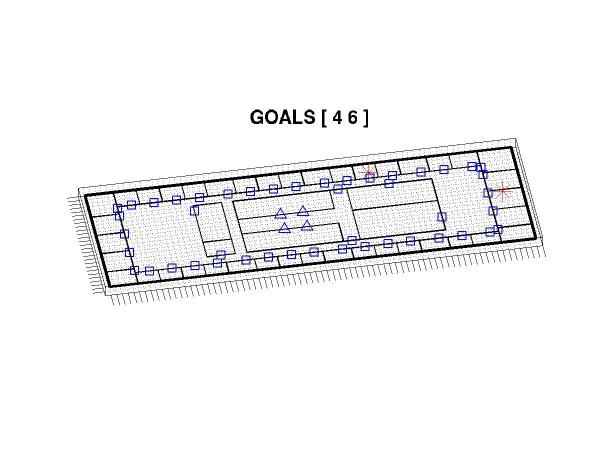
In this page, we'll focus on reward decompositions; for an overview of the roles of some of these other ideas, you can examine our IJCAI workshop paper.

An Example Problem

Consider the following maze world, roughly modeled after the seventh floor of the Artificial Intelligence lab building at MIT (this is actually a small subset of the package delivery problem). The blue squares indicate the locations of doors and the blue triangles indicate the elevators; black lines are impermeable walls. Under a simplistic model of robot navigation, the agent can move in any of the cardinal directions with high probability of success (0.9 in this world dynamic), except where blocked by walls or locked doors. When the robot fails to move in the desired direction, it finds itself in another (accessible) adjacent cell with uniform probability.

Goal-Oriented Planning

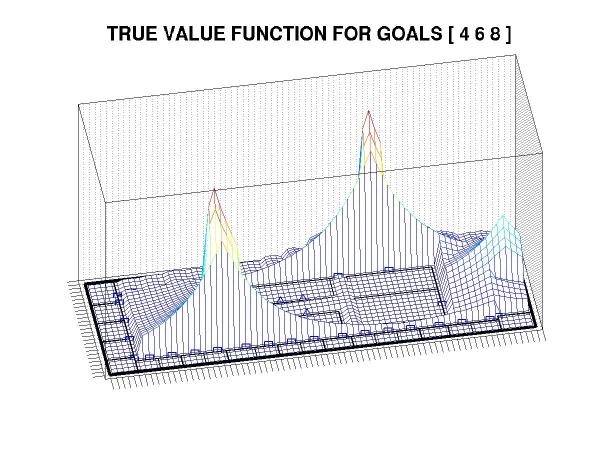
Suppose that we wish the robot to deliver packages to the two locations denoted with red asterisks in the map. In an MDP framework, we associate a reward with each goal state and plan a course of action so as to maximize the expected total reward. Notably, in standard techniques all reward sources are integrated simultaneously and the resulting plan depends on the precise relationships of reward magnitudes between the different goals. We are, instead, interested in approaches to decomposing the reward function into components associated with individual sub-goals. For example, a goal-specific plan (also known as a macro action or, more generally, an option) for reaching goal state 4 would look like:

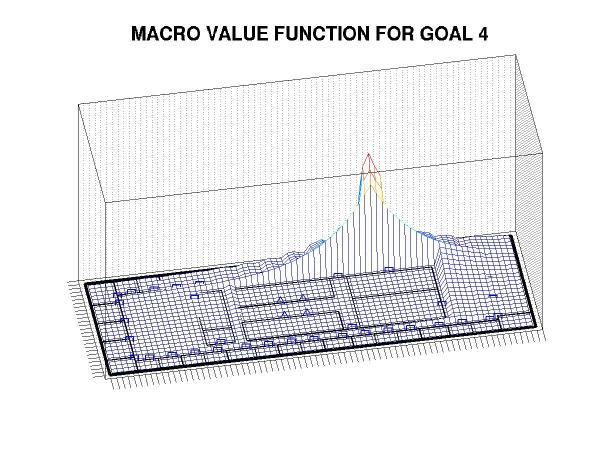
Technically, this structure is a value function, which represents the expected discounted reward achievable from each state by following the policy; in essence, the agent follows the gradient of this function to seek a goal state. For more details on the relationships of plans to value functions, see Puterman's text.

Similarly, a plan for achieving the sub-goal associated with state 6 looks like:

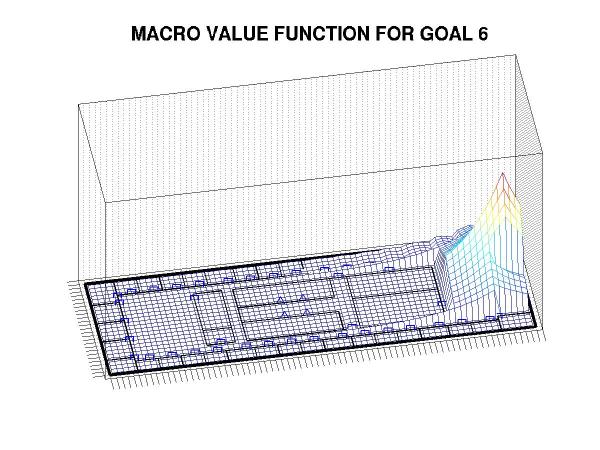
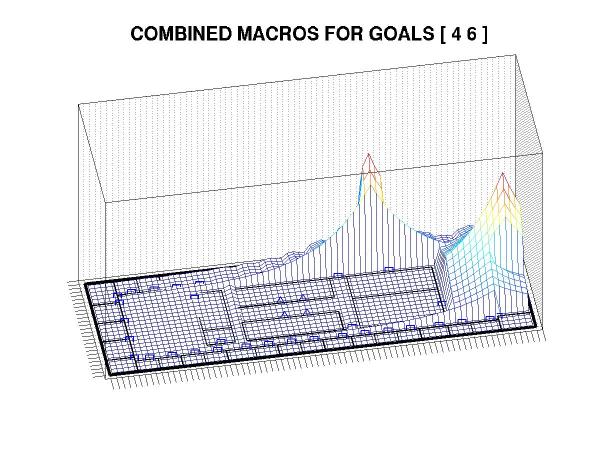
The issue now becomes properly integrating the two macros. With standard MDP planning techniques, we would be forced to create a completely new plan that considers both goal states simultaneously at a cost equivalent to the creation of each of the two individual sub-goals. We propose a method that employs the already generated macros and makes completely local decisions to produce an integrated plan at runtime:
This integrated plan was produced in 0.18 seconds while the direct solution of the MDP required more than a minute.

Furthermore, we can easily change the relative weights of the goal states in response to changing environmental demands. This plot would again require a full recomputation of the MDP but we produce it cheaply, using only the cached macros for the individual goal states:

We can even add additional goals. If the new goal was known at initialization time, we will have cached a macro for achieving it, but if not we can compute that macro now at no greater cost than would have been incurred by solving this unique MDP situation directly. Thereafter, of course, we do have access to this macro and can take this goal state into account easily.
In addition, because we plan using purely local information, it is not necessary to fully construct an explicit representation of the plan. The agent can select actions on-demand as it reaches each state and, in fact, the rewards can be changed between each action with no computational penalty (though such a world is extremely non-stationary and any plan derived from standard MDP solutions is likely to be highly sub-optimal).

The Catch: Suboptimal Planning Performance

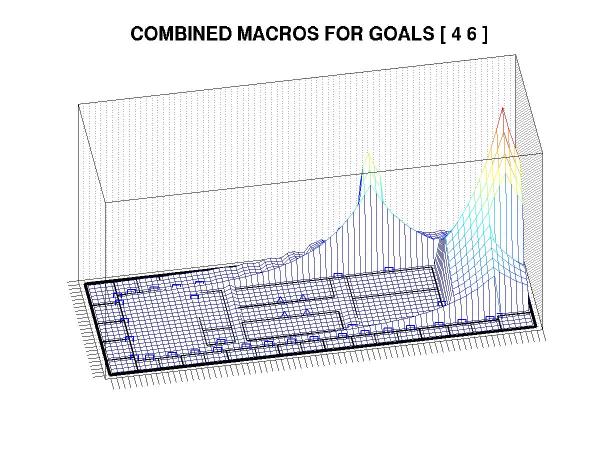
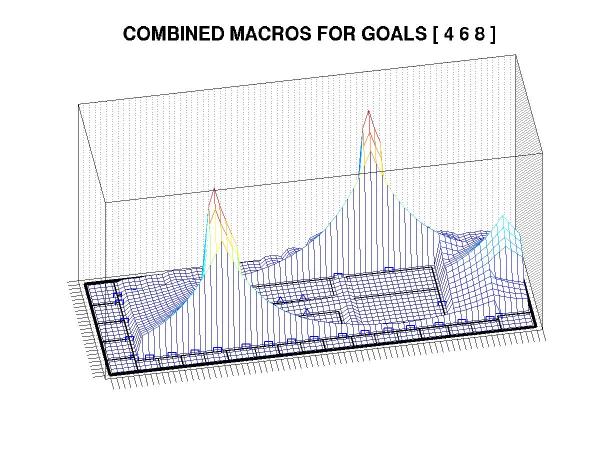
Of course, it really would be too much to hope that we could get all of that for free. The nearly inevitable catch is that this approach can produce sub-optimal plans -- sometimes substantially so. The fundamental problem is that the goal states interact in complex ways and, in general, the problem of trading off between different goals can be NP-hard (more specifically, if you have to achieve a number of different goal states in succession and need to decide what order to take them in, then you're effectively dealing with the TSP). Such decisions cannot (to the best of anyone's knowledge) be resolved purely with local information, so it's some consolation to realize that suboptimality is inevitable given the runtime constraints that we've applied.

There is, however, still the question of just how suboptimal a plan our heuristic produces. It is not yet clear whether we can bound this quantity, though we have evidence to indicate that the loss is generally small. For example, here is the exact plan corresponding to the last example, above:

The visual difference between this and our approximate plan is nearly undetectable while the measurable difference (normalized Bellman error, a.k.a. regret) is less than 0.5%.