Fast example-based pose estimation
The objective of articulated pose estimation is to infer location and
orientation of artuculated object's body parts (the level of refinement and the accuracy of
description depends on the task at hand). The most common, and perhaps
the most important, instance of this problem is the estimation of
human articulated pose: the goal here is to understand the "posture"
of the person. The images below illustrate this: basically, our goal
is to have a computer look at the image on the left and infer all the
information it needs to render the figure on the right,
showing a synthetic character in the same body posture as the person
on the left.
Parameter-Sensitive Hashing (PSH) is an algorithm for fast similarity
search for regression tasks, when the goal is to find examples in the
database which have values of some parameter(s) similar to those of
the query example, but the parameters can not be directly computed
from the examples.
Locality Sensitive Hashing
PSH is essentially an adaptation of Locality-Sensitive Hashing
(LSH)
algorithm by Indyk and
Motwani. Below is a very coarse summary of LSH; please refer to the LSH website
and the original LSH papers for more complete explanations.
Assume that the data live in an N-dimensional integer
space, and all the values are in the range [0,C] (note that for any finite size data set these assumptions can
be enforced by applying suitable transformation on the data).
The algorithm uses (conceptually - there is no need to actually
compute it) unary encoding of the data: if an
integer x is known to be between 0 and C than its value can be
encoded by C bits, where bit i is 0 if and only if
x<i.
Consider a very simple hash function, with only two buckets,
which is constructed randomly: select a random dimension n from
[1,N] and a random value c from [1,C], and take
the c-th bit from the unary encoding of the n-th
dimension of an example x. This is essentially a
decision stump. It's illustrated in the figure below: any point
above the line is mapped to 1, any point below to 0.
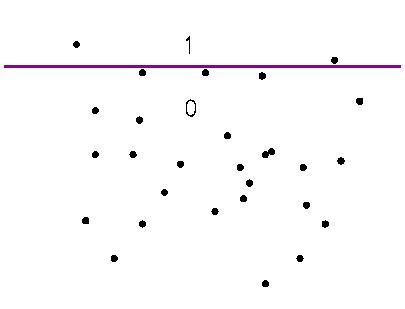
It can be shown that such a
one-bit hash function is locality sensitive: two examples that
are close to each other are more likely to fall to the same bucket (i.e.,
on the same side of the decision stump), and two examples which are
far from each other are more likely to be separated. The odds here can
be very mild, but this is improved in the next step.
Now consider a k-bit hash functions constructed by randomly
selecting k 1-bit functions as described above and
concatenating the bits they produce. This hash function maps the data
into 2k buckets. The probability of "good"
collision (points that are close falling in the same bucket) is
somewhat lower now, but the probability of "bad" collision is much
lower. A hash table like that is illustrated in the figure below; the
order of the stumps correspond to increasing bit significance order. Note
that some of the buckets are always empty, e.g., 1101 is impossible
since it would imply "left of (3) AND right of (4)".
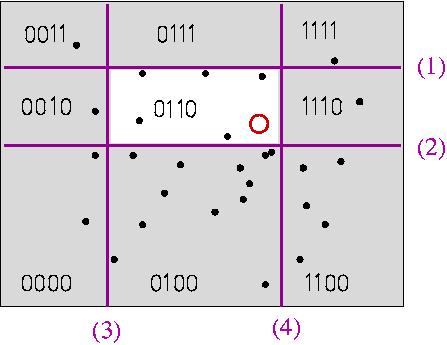
For given values of the parameters k and l, LSH
constructs l hash functions with k bits as described
above. In the figure below, you can see two four-bit hash functions
(the magenta one from before, and the green one). When a query comes in, it is mapped to a bucket in each of the
hashtables, and the union of the "winning" buckets (shaded area in the
figure below) is searched to find
the examples that are close enough to the query, or the closest one(s)
- depending on the objective of the task.
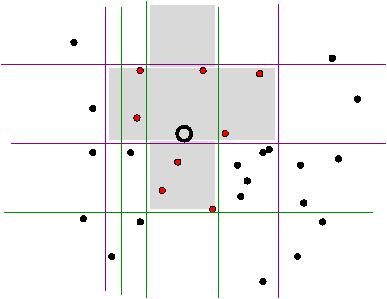
This is of course an approximate similarity search, in the sense
that we may miss the answer even if it exists in the database, however
this happens with probability which can in practice be made
arbitrarily small. Please see the LSH literature to learn about the guarantees on
running time and probability of success of this algorithm.
Parameter Sensitive Hashing
It is clear how LSH can be applied to search in a space where all we
care about is the
The main idea of PSH is to find a feature space (i.e., a
transformation of the image) in which the
similarity in terms of L1
distance would be closely related to similarity in parameter (in our
case, pose) space. Seen in this way, illustrated below, a decision
stump at the value T on feature φ is acting as
a paired classifier - applied on a pair of images, it
"classifies" the two images as having a similar pose if both of them fall on the same side
(blue dots), or as having sufficiently different poses if they are
separated (red dots).
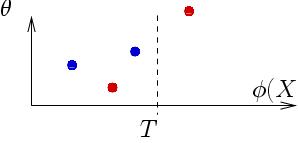
Given a training set of images with known poses (our database), we
automatically also have a huge set of image pairs with known
labels: we can label a pair as positive if the poses in the two images
are close enough. Just what is considered close enough depends on the
application needs. In our experiment, we decided that poses which
correspond distances less than 5cm between key body joints (in 3D) are
close enough. Below is an example of a positive pair and a negative pair.
As you can see, these are not real people. We used Poser® to
generate a databes of 500,000 images like the ones above, with a
variety of clothing, hair, face and lighting conditions.
Now we are faced with a straighforward learning task: select the
decision stumps that have precision better than some minimum on this
classification task. Parameter-Sensitive Hashing then proceeds with
Combining a number of such decision stumps into a k-bit hash
table makes a more complex
classifier, which assigns a positive label to a pair such that both of
the images fall in the same bucket. To those who are familiar with the
idea of boosting (building a strong ensemble classifier from a set of
so-called weak learners, each of which may be only slightly better
than random) this may sound familiar. This analogy led us to develop a
boosting-based approach to PSH: we learn the decision stumps in a
greedy fashion, explicitly increasing the performance of the
hashing. This is described in the CMU tech. report linked below.
Publications:
- G. Shakhnarovich, P. Viola, T. Darrell. Fast pose estimation with
Parameter-Sensitive Hashing - presented at ICCV 2003
- Also, take a look at this reference, which describes a more recent
piece of related work:
L. Ren, G. Shakhnarovich, J. Hodgins, P. Viola, H. Pfister. Learning
Silhouette Features for Control of Human Motion - accepted
(pending revision) to ACM Transactions on Graphics, in the meantime
available as a CMU Technical Report. This is a description of the
work done in collaboration with CMU and MERL, in which our approach to
pose estimation is extended to create a real-time motion-driven interface to
animation (swing dance). Among key new contributions are the
AdaBoost-based greedy learning of similarity classifiers, the direct use of
Hamming space embedding for classifying pairs, and the combination
with motion context by integrating the single-frame estimation with
the motion graph. Liu Ren demonsrated this system at SIGGRAPH 2004.







