3.1 Micro-benchmarks
We use a variety of microbenchmarks to test read and write latencies for different scenarios. At the highest level, a read/write is classified as to a private variable (accessed using a standard load/store) or a shared variable (accessed through a call to the Split-C library). Accesses to shared variables are further classified based on whether the read/write is to a local block (i.e. the requesting node is also the home node) or a remote block (the requesting node is not the home node). The accesses are further classified by what state the block is in on the requesting node and what state the block is in at the home.The resulting latencies are shown below in Figures 6 and 7. The microbenchmarks access 32 bit integer variables, and the SWCC block size is 8 bytes. The standard Split-C access times for local and remote variables can be compared to the SWCC-Split-C times for the various flavors of each kind of access. Note that the microbenchmarks are designed to give average access times without distinguishing between processor hardware cache hits and misses.
As expected, the software cache coherence protocols add some overhead to shared variable accesses which are local; these latencies are about 2 to 5 times that of standard Split-C. Additionally, an access to a variable which another processor has obtained in the modified state is several orders of magnitude longer because the block must be fetched with a network transaction. When a local shared variable is accessed whose block has not been accessed by any other node (the state is invalid, i.e. not present), our previously described optimizations allow us to satisfy the request in the nodes local memory after a single check in directory hash table. This has a significant performance advantage, and the access takes less than half the time of one which must go to a directory entry. In this case we also don't have to create a new directory entry the first time the variable is accessed, which can take as long as 50us.
The real win comes when a shared variable is accessed whose home is on a remote processor but that is in an appropriate state in the local directory. In this case, SWCC-Split-C satisfies the request locally, while standard Split-C must conduct a network transaction which takes two orders of magnitude longer.
When SWCC-Split-C must go to the home node to satisfy a request, the transaction takes about 50us if the home node has the block in an appropriate state to return to the local node without conducting network transactions with remote nodes. One reason this time is significantly longer than the 30us for standard Split-C is that our implementation uses medium-sized Active Messages to transfer the data block, while standard Split-C uses a short AM to send the variable. Medium-sized Active Messages are designed for send large blocks of data and optimizing for throughput, while short Active Messages optimize for latency [7].
When the home node must send invalidate or flush messages to remote nodes, the latency is about twice as long, depending on the types of messages which must be sent.
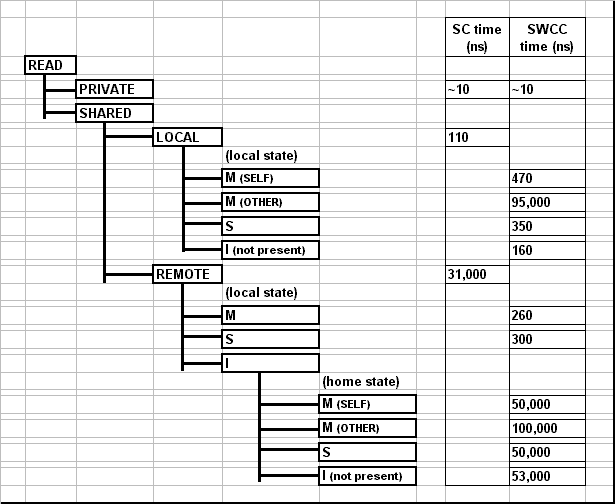
Figure 6: Read Micro-Benchmark Results
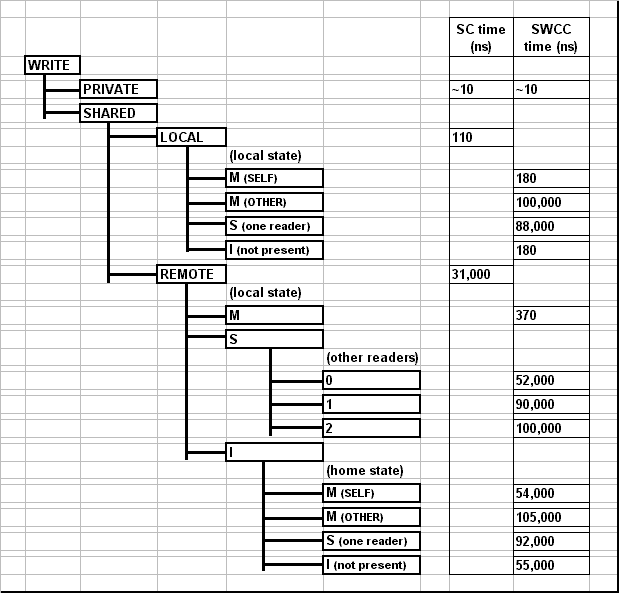
Figure 7: Write Micro-Benchmark Results
Here, the multiply is blocked to take advantage of locality within the
data. Note that it is not coded for locality across processors. The
code uses a bulk split-phase read (bulk_get) to optimize the memory
transaction. "matrix_mult" is a call to a local matrix multiply
written in c. For the SWCC version, we read the data back into a
global array after doing the local matrix multiply. The Split-C
kernel of the blocked matrix multiply is given below:
This version of the matrix multiply is identical to the previous
version except the local matrix multiply has been hand optimized at
the level of assembly code.
Figure 8 below shows the result of the naive matrix multiplication
algorithm on 128x128 square matrices with a varying number of
processors. The peak rate for this algorithm using a sequential c
version on a single processor is about 3.5 MFLOPS. The standard
Split-C version is completely dominated by remote memory accesses.
The lowest line in the plot shows the expected performance for a
matrix multiplication dominated by a 30us read access time, and the
standard Split-C version performs only slightly better than this.
The SWCC-Split-C versions take advantage of the redundant memory
references, and all perform significantly better than the
standard Split-C version. With increasing block size, the performance
of the SWCC versions improves due to spatial locality as expected;
this effect is shown in Table 1. The
maximum rate achieved by the SWCC versions is about 1 MFLOP per
processor. This is significantly lower than the sequential version
due to the cost of the initial remote fetch of a block, and the
protocol overhead after the block is cached locally.
Scaling the Matrix Size
Next we examine scaling the matrix dimensions with a fixed number of
processors. Figure 9 below shows the performance results of using 8
processors to multiply square matrices of varying dimensions.
For a naive matrix multiplication of dimension d, the proportion of the
total memory reads which are redundant is proportional to d. Thus, as
the matrix size is increased, the SWCC read hit percentage goes up as
shown in Table 2 below. This behavior causes the local hit time
to dominate the performance rather than the
remote miss time. In Figure 9, the standard Split-C version achieves
no performance improvement because it does not benefit from redundant
memory accesses. The SWCC versions do take advantage of the redundant
memory reads, and they all improve with increasing matrix dimensions.
We can calculate the predicted ideal MFLOP rate by assuming all reads
and writes are SWCC hits. Based on the data from the
Micro-Benchmarks, reads take approximately 350ns, and writes take
about 180ns. Matrix multiply using standard Split-C on a single
processor achieves a rate of 3 MFLOPS, so we estimate that floating
point operations along with additional overhead cost 333ns. The ideal
rate should then be 1/(Tf + Trd + Twr/2), which is 1.3 MFLOPS per
processor. The SWCC versions in Figure 9 approach 1 MFLOP per
processor which is a reasonable margin of error from the calculated
ideal rate.
We don't know why performance drops off with the largest matrix
dimension for the 64 and 256 byte block size versions. There are more
directory entries needed with larger matrices; for example with a 256 byte
block size, each processor creates 2056 directory entries for 256x256
matrix multiply
compared to 8200 directory entries for 512x512 matrix multiply. However, the
directory hash table was always big enough to have every entry pointed to
directly by the hash table (instead of through a linked list).
Still, with more directory entries, the entry pointers will cause more
conflicts in the processors L1 hardware cache, which will impact
performance. Also, each processor will have to service more block
requests from other processors, which will take cycles away from the
local program and likewise hurt performance. Or there might be
problems with network traffic due to the increased number of messages.
Figure 10 below shows the performance of increasingly optimized
various versions of matrix multiply. Note that the versions on the
x-axis of the plot are arbitrary, there is no numerical order to the
progression. Also note that the y-axis is a log scale.
For the blocked versions, one thing to note is that the blocks are
read with a Split-C bulk_get operation. Standard Split-C divides bulk
transactions into medium sized Active Messages, but our implementation
of SWCC-Split-C divides them up into block size transactions. For the
implementation of Active Messages which we use, the medium AM size is
8192, so swcc_8192 is the only really useful basis for comparison.
As shown before, the SWCC performs an order of magnitude
better than standard Split-C for the naive version. For blocked
matrix multiply with block size b*b, the redundant references are
reduced by a factor of b; this affect is shown in Table 3 by the
decreasing hit ratio. Due to this decrease, SWCC-Split-C has less
opportunity to out-perform Split-C, although swcc_8192 does do better
in several cases.
This application models the interaction of electric and magnetic fields on
a 3-d object. The program used for benchmarking is actually a simplified
version, using a randomly generated graph instead of an actual object to
generate the fields and node dependencies. However, it is an accurate
representation, as the EM3D application is in practice quite irregular.
This makes it difficult for
the application programmer to program for locality, possibly making a
cached system more desirable.
The em3d application takes several parameters:
The application first builds a random graph based on the parameters
specified. Each processor is allocated number of nodes e nodes and
number of nodes h nodes. For each node, a dependence count is
randomly generated, with an average dependence count of degree of
nodes. For each dependence, a node to be depended on is selected.
First, the remote probability parameter is used to determine if the
node to be depended on is remote or local. If it is remote, the
dist_span parameter is used to determine on which processor the
node should depend on. A random node is then selected from that
processor. Note that h nodes only depend on e nodes, and e nodes only
depend on h nodes, allowing the computation to be broken into two phases.
Once the graph is created, the main loop is entered:
For EM3D measurements, each configuration was run 5 times and the average
time/iteration was measured. For each run, the number of
iterations was 10 and the dist_span was set to 1.
It should be noted that the parameters used may not necessarily be
representative of real EM3D problem sets. However, the setup is still
useful as a general model of how many parallel programs may
communicate.
Scaling Remote Dependency Probability
We first examined the effect that the remote probability had on the
applications. Figure 11 below shows the results of an EM3D test with
8 processors, in which each processor has 500 nodes and each node has
an average of 40 dependencies. We set the distance span to 1
in order to increase the number of common dependencies which nodes on
a processor share.
As the remote probability increases, the number of remote reads
that each processor does increases; this effect is demonstrated in
Table 4. This is why the running time of the standard Split-C
version of EM3D scales linearly with the percentage of remote
dependencies.
The advantage that the SWCC versions have is that, increasing the
percentage of remote dependencies also increases the
probability that two or more nodes on a given processor will depend on
the same remote node. This means that once the value of the remote
node has been obtained, future accesses will be software cache hits
rather than remote memory accesses. Since each processor has a
constant number of nodes, the collection of dependencies of the nodes
owned by one processor will eventually include every node owned by its
neighboring processors. Once this happens, increasing the remote
probability will not increase the total number of nodes depended
on by the collection of nodes owned by a single processor. This means
that the number of remote memory transactions per iteration remains
constant, which is why the curves in Figure 11 become flat.
One disadvantage of caching is that at the end of each iteration, a
processor must send out invalidate Requests before it
can update its nodes which have been read by other processors. A way
to avoid this problem is to send updates instead of
invalidates at the end of each iteration; this option was
explored with Stache [9].
The reason that the SWCC 1024 and 8192 versions perform worse than
those with smaller block sizes seems to be an interesting form of
false sharing. As described previously, our protocol implementation
optimizes shared variable accesses which are local to a processor and
for which the software cache block has not been accessed by any other
processor. The frequency of this type of access in the EM3D program
is shown in Table 5. As the block size increases, it becomes
more likely that shared variables which are only used by the owning
processor will lie within blocks that are accessed by other
processors. This will increase the latency for accessing these
variables, and thereby impact performance. Better data layout could
potentially alleviate this problem.
Scaling Number of Processors
We next look at how the application scales as the number of processors
increases. Remember that the problem size scales with the processors, so
the computation per processor remains constant. As the number of
processors is increased, the amount of network transactions increases.
We fix the percentage of remote dependencies as 24/40, and vary
the number of processors from 2 to 16, as shown in Figure 12 below.
Figure 12: EM3D, Number of Processors vs. Time
The SWCC configurations with small block size outperform
standard Split-C for each processor configuration tested. It is
interesting that the standard Split-C implementation reaches a
constant Time/Iter, while the SWCC versions continue to increase.
This effect actually seems to be an artifact of our implementation.
In our EM3D code, Processor 0 initializes all of the node values.
This part of the application isn't timed, but it does cause Processor
0 to obtain all of the shared blocks in a modified state. Then
during the first iteration of EM3D, there is contention at Processor 0
for the shared values which scales with the number of processors.
Presumably, this one-time effect would diminish with more iterations
of EM3D.
3.2 Matrix Multiply
This application does a matrix multiply: C = A x B. Each matrix
is made up of 64bit doubles, and is
spread across the processors; each processor is responsible for
computing its own portion of the result matrix. There are 3
versions ranging from the most naive implementation to a highly
optimized, blocked implementation. We show the performance advantage
of software cache coherence for the naive version, and evaluate the
advantage of caching as the application becomes more optimized. The
varying levels of optimization are described below.
3.2.1 Versions
Naive
This is the simplest implementation of matrix multiply. It does
stagger the starting point for the vector vector dot products that
makes up the inner loop, but it ignores
locality, both within a processor and across processors. The Split-C
kernel of the naive matrix multiply is given below:
for_my_2D(i,j,l,n,m) {
double sum = C[i][j];
kk = MYPROC%r;
for (k=0;k < r;k++) {
sum = sum + A[i][kk]*B[kk][j];
kk++;
if (kk==r) kk=0;
}
C[i][j] = sum;
}
Blocked
for_my_2D(i,j,l,n,m) {
double (*lc)[b] = tolocal(C[i][j]);
kk = 0;
for (k=0;k < r;k++) {
bulk_get (la, A[i][kk], b*b*sizeof(double));
bulk_get (lb, B[kk][j], b*b*sizeof(double));
sync();
matrix_mult(b,b,b,lc,la,lb);
kk++; if (kk==r) kk=0;
}
#ifdef SWCC
for (ii=0; ii < b; ii++) {
for (jj=0; jj < b; jj++) {
C[i][j][ii][jj] = lc[ii][jj];
}
}
#endif
}
Optimized Blocked
3.2.2 Algorithm Analysis
In a square matrix multiplication of dimension d, there are
2d3 floating point operations, 2d3 reads, and
d3 writes.
Thus, the MFLOP rate is approximately
2d3/(2d3*Tf + 2d3*Trd +
d3*Twr) =
1/(Tf + Trd + Twr/2),
where Tf, Trd, and Twr are the average times for a floating point
operation, a read, and a write respectively.
The data set size for the reads is 2d2, so the number of
redundant reads is (2d3 - 2d2).
For a blocked matrix multiply with square blocks of size b, the number
of redundant reads is reduced by a factor of b.
3.2.2 Performance Results
Scaling the Number of Processors
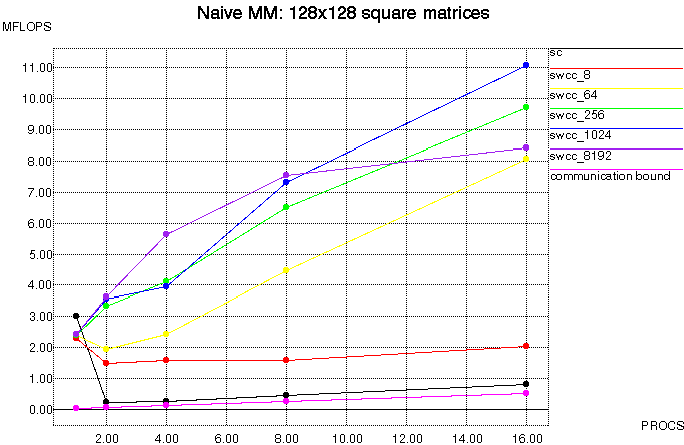
Figure 8: Naive Matrix Multiply, 128x128 square matrices, aggregate
MFLOPS vs. number of processors.
shared reads / processor
%hits
# of misses
swcc_8
229377
97.28
2048
swcc_256
229377
99.91
65
swcc_8192
229377
99.99
3
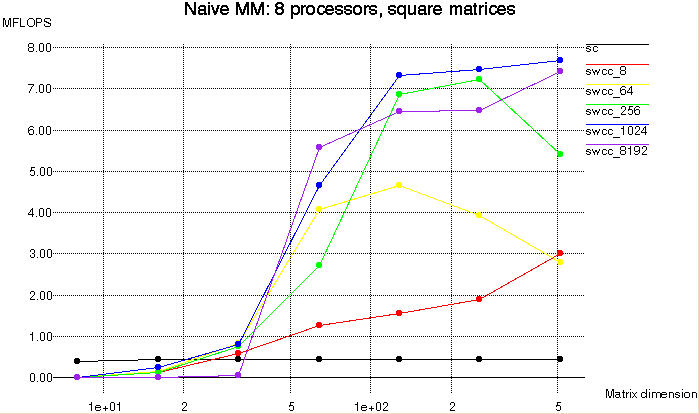
Figure 9: Naive Matrix Multiply, square matrices, 8
processors, aggregate MFLOPS vs. matrix dimension.
shared reads / processor
%remote
%hits
8x8
136
41.18
86.03
16x16
1056
42.42
98.67
32x32
8320
43.08
99.58
64x64
66048
43.41
99.82
128x128
526336
43.58
99.91
256x256
4202496
43.66
99.96
512x512
33587200
43.71
99.98
Varying the Algorithm
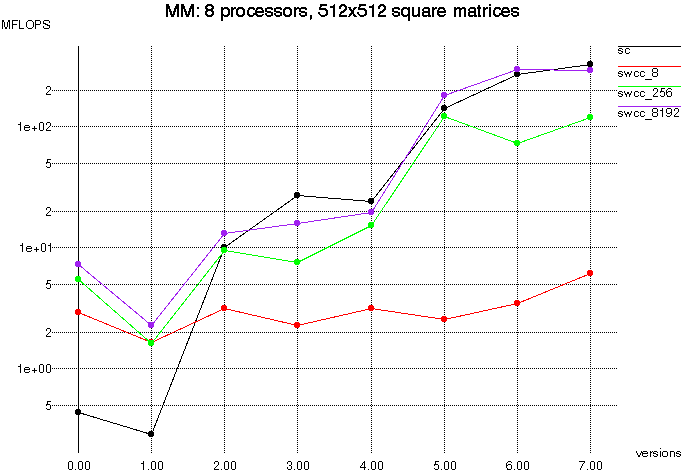
Figure 10: Matrix Multiplication, 512x512 element matrix, 8
processors, various versions:
Version 0 =
naive
Version 1 =
blocked, 1x1 element blocks (512x512 blocked matrix)
Version 2 =
blocked, 4x4 element blocks (128x128 blocked matrix)
Version 3 =
blocked, 16x16 element blocks (32x32 blocked matrix)
Version 4 =
blocked, 64x64 element blocks (8x8 blocked matrix)
Version 5 =
optimized blocked, 16x16 element blocks (32x32 blocked matrix)
Version 6 =
optimized blocked, 64x64 element blocks (8x8 blocked matrix)
Version 7 =
optimized blocked, 128x128 element blocks (4x4 blocked matrix)
shared reads / processor
%remote
%hits
naive
33587200
43.71
99.98
blocked 1x1
33554432
43.75
99.97
blocked 4x4
786432
43.75
98.92
blocked 16x16
73728
43.75
88.45
blocked 64x64
16512
43.75
50.05
blocked 128x128
8208
62.50
31.30
3.3 EM3D
Note that the number of nodes denotes how many nodes each processor has.
Thus, the computation scales as the number of processors scales.
for(numIters)
{
compute_e_nodes(...);
barrier();
compute_h_nodes(...);
barrier();
}
Here, each processor computes the new values for the nodes it owns. To do
this, the dependence list of each node is traversed. Since the nodes may
depend on remote nodes, this step may cause remote reads. Note that since
each processor computes only its nodes new values, there are no remote
writes in the main loop.
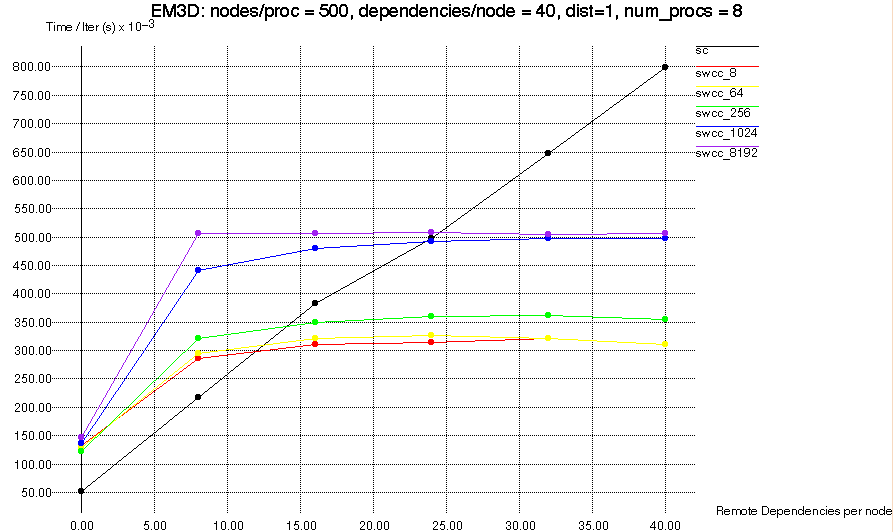
Figure 11: EM3D, Remote Dependencies vs. Time
shared reads
%remote
swcc_8 %hits
swcc_256 %hits
swcc_8192 %hits
0
1160711
0.00
99.83
99.91
100.00
8
1160711
3.58
98.99
99.07
99.82
16
1160711
7.14
98.98
99.05
99.82
24
1160711
10.68
98.98
99.05
99.82
32
1160711
14.23
98.98
99.05
99.82
40
1160711
17.85
98.98
99.05
99.82
unshared local read hit%
unshared local write hit%
swcc_8
31.13
15.99
swcc_64
29.70
15.26
swcc_256
23.26
11.95
swcc_1024
11.36
5.83
swcc_8192
0.02
0.01
We can see that the original Split-C version, sc, scales linearly
with the number of remote dependencies. The various SWCC
versions have more overhead when there are few remote
dependencies. However, once there are more than about 8 remote
dependencies per node, the time/iteration is almost constant.
With more than 12 remote dependencies per node, the SWCC 8, 64,
and 256 versions outperform standard Split-C, as do the 1024 and 8192
versions when there are more than 24 remote dependencies per node.
[Prev]
[Next]
[Index]