Back to Item 15: Understand the costs of exception handling   
  Continue to Item 16: Remember the 80-20 rule.

Efficiency

I harbor a suspicion that someone has performed secret °Pavlovian experiments on C++ software developers. How else can one explain the fact that when the word "efficiency" is mentioned, scores of programmers start to drool?

In fact, efficiency is no laughing matter. Programs that are too big or too slow fail to find acceptance, no matter how compelling their merits. This is perhaps as it should be. Software is supposed to help us do things better, and it's difficult to argue that slower is better, that demanding 32 megabytes of memory is better than requiring a mere 16, that chewing up 100 megabytes of disk space is better than swallowing only 50. Furthermore, though some programs take longer and use more memory because they perform more ambitious computations, too many programs can blame their sorry pace and bloated footprint on nothing more than bad design and slipshod programming.

Writing efficient programs in C++ starts with the recognition that C++ may well have nothing to do with any performance problems you've been having. If you want to write an efficient C++ program, you must first be able to write an efficient program. Too many developers overlook this simple truth. Yes, loops may be unrolled by hand and multiplications may be replaced by shift operations, but such micro-tuning leads nowhere if the higher-level algorithms you employ are inherently inefficient. Do you use quadratic algorithms when linear ones are available? Do you compute the same value over and over? Do you squander opportunities to reduce the average cost of expensive operations? If so, you can hardly be surprised if your programs are described like second-rate tourist attractions: worth a look, but only if you've got some extra time.

The material in this chapter attacks the topic of efficiency from two angles. The first is language-independent, focusing on things you can do in any programming language. C++ provides a particularly appealing implementation medium for these ideas, because its strong support for encapsulation makes it possible to replace inefficient class implementations with better algorithms and data structures that support the same interface.

The second focus is on C++ itself. High-performance algorithms and data structures are great, but sloppy implementation practices can reduce their effectiveness considerably. The most insidious mistake is both simple to make and hard to recognize: creating and destroying too many objects. Superfluous object constructions and destructions act like a hemorrhage on your program's performance, with precious clock-ticks bleeding away each time an unnecessary object is created and destroyed. This problem is so pervasive in C++ programs, I devote four separate items to describing where these objects come from and how you can eliminate them without compromising the correctness of your code.

Programs don't get big and slow only by creating too many objects. Other potholes on the road to high performance include library selection and implementations of language features. In the items that follow, I address these issues, too.

After reading the material in this chapter, you'll be familiar with several principles that can improve the performance of virtually any program you write, you'll know exactly how to prevent unnecessary objects from creeping into your software, and you'll have a keener awareness of how your compilers behave when generating executables.

It's been said that forewarned is forearmed. If so, think of the information that follows as preparation for battle.

Back to Efficiency   
  Continue to Item 17: Consider using lazy evaluation

Item 16:  Remember the 80-20 rule.

The 80-20 rule states that 80 percent of a program's resources are used by about 20 percent of the code: 80 percent of the runtime is spent in approximately 20 percent of the code; 80 percent of the memory is used by some 20 percent of the code; 80 percent of the disk accesses are performed for about 20 percent of the code; 80 percent of the maintenance effort is devoted to around 20 percent of the code. The rule has been repeatedly verified through examinations of countless machines, operating systems, and applications. The 80-20 rule is more than just a catchy phrase; it's a guideline about system performance that has both wide applicability and a solid empirical basis.

When considering the 80-20 rule, it's important not to get too hung up on numbers. Some people favor the more stringent 90-10 rule, and there's experimental evidence to back that, too. Whatever the precise numbers, the fundamental point is this: the overall performance of your software is almost always determined by a small part of its constituent code.

As a programmer striving to maximize your software's performance, the 80-20 rule both simplifies and complicates your life. On one hand, the 80-20 rule implies that most of the time you can produce code whose performance is, frankly, rather mediocre, because 80 percent of the time its efficiency doesn't affect the overall performance of the system you're working on. That may not do much for your ego, but it should reduce your stress level a little. On the other hand, the rule implies that if your software has a performance problem, you've got a tough job ahead of you, because you not only have to locate the small pockets of code that are causing the problem, you have to find ways to increase their performance dramatically. Of these tasks, the more troublesome is generally locating the bottlenecks. There are two fundamentally different ways to approach the matter: the way most people do it and the right way.

The way most people locate bottlenecks is to guess. Using experience, intuition, tarot cards and Ouija boards, rumors or worse, developer after developer solemnly proclaims that a program's efficiency problems can be traced to network delays, improperly tuned memory allocators, compilers that don't optimize aggressively enough, or some bonehead manager's refusal to permit assembly language for crucial inner loops. Such assessments are generally delivered with a condescending sneer, and usually both the sneerers and their prognostications are flat-out wrong.

Most programmers have lousy intuition about the performance characteristics of their programs, because program performance characteristics tend to be highly unintuitive. As a result, untold effort is poured into improving the efficiency of parts of programs that will never have a noticeable effect on their overall behavior. For example, fancy algorithms and data structures that minimize computation may be added to a program, but it's all for naught if the program is I/O-bound. Souped-up I/O libraries (see Item 23) may be substituted for the ones shipped with compilers, but there's not much point if the programs using them are CPU-bound.

That being the case, what do you do if you're faced with a slow program or one that uses too much memory? The 80-20 rule means that improving random parts of the program is unlikely to help very much. The fact that programs tend to have unintuitive performance characteristics means that trying to guess the causes of performance bottlenecks is unlikely to be much better than just improving random parts of your program. What, then, will work?

What will work is to empirically identify the 20 percent of your program that is causing you heartache, and the way to identify that horrid 20 percent is to use a program profiler. Not just any profiler will do, however. You want one that directly measures the resources you are interested in. For example, if your program is too slow, you want a profiler that tells you how much time is being spent in different parts of the program. That way you can focus on those places where a significant improvement in local efficiency will also yield a significant improvement in overall efficiency.

Profilers that tell you how many times each statement is executed or how many times each function is called are of limited utility. From a performance point of view, you do not care how many times a statement is executed or a function is called. It is, after all, rather rare to encounter a user of a program or a client of a library who complains that too many statements are being executed or too many functions are being called. If your software is fast enough, nobody cares how many statements are executed, and if it's too slow, nobody cares how few. All they care about is that they hate to wait, and if your program is making them do it, they hate you, too.

Still, knowing how often statements are executed or functions are called can sometimes yield insight into what your software is doing. If, for example, you think you're creating about a hundred objects of a particular type, it would certainly be worthwhile to discover that you're calling constructors in that class thousands of times. Furthermore, statement and function call counts can indirectly help you understand facets of your software's behavior you can't directly measure. If you have no direct way of measuring dynamic memory usage, for example, it may be helpful to know at least how often memory allocation and deallocation functions (e.g., operators new, new[], delete, and delete[] — see Item 8) are called.

Of course, even the best of profilers is hostage to the data it's given to process. If you profile your program while it's processing unrepresentative input data, you're in no position to complain if the profiler leads you to fine-tune parts of your software — the parts making up some 80 percent of it — that have no bearing on its usual performance. Remember that a profiler can only tell you how a program behaved on a particular run (or set of runs), so if you profile a program using input data that is unrepresentative, you're going to get back a profile that is equally unrepresentative. That, in turn, is likely to lead to you to optimize your software's behavior for uncommon uses, and the overall impact on common uses may even be negative.

The best way to guard against these kinds of pathological results is to profile your software using as many data sets as possible. Moreover, you must ensure that each data set is representative of how the software is used by its clients (or at least its most important clients). It is usually easy to acquire representative data sets, because many clients are happy to let you use their data when profiling. After all, you'll then be tuning your software to meet their needs, and that can only be good for both of you.

Back to Item 16: Remember the 80-20 rule   
  Continue to Item 18: Amortize the cost of expected computations

Item 17:  Consider using lazy evaluation.

From the perspective of efficiency, the best computations are those you never perform at all. That's fine, but if you don't need to do something, why would you put code in your program to do it in the first place? And if you do need to do something, how can you possibly avoid executing the code that does it?

The key is to be lazy.

Remember when you were a child and your parents told you to clean your room? If you were anything like me, you'd say "Okay," then promptly go back to what you were doing. You would not clean your room. In fact, cleaning your room would be the last thing on your mind — until you heard your parents coming down the hall to confirm that your room had, in fact, been cleaned. Then you'd sprint to your room and get to work as fast as you possibly could. If you were lucky, your parents would never check, and you'd avoid all the work cleaning your room normally entails.

It turns out that the same delay tactics that work for a five year old work for a C++ programmer. In Computer Science, however, we dignify such procrastination with the name lazy evaluation. When you employ lazy evaluation, you write your classes in such a way that they defer computations until the results of those computations are required. If the results are never required, the computations are never performed, and neither your software's clients nor your parents are any the wiser.

Perhaps you're wondering exactly what I'm talking about. Perhaps an example would help. Well, lazy evaluation is applicable in an enormous variety of application areas, so I'll describe four.

Reference Counting

Consider this code:

A common implementation for the String copy constructor would result in s1 and s2 each having its own copy of "Hello" after s2 is initialized with s1. Such a copy constructor would incur a relatively large expense, because it would have to make a copy of s1's value to give to s2, and that would typically entail allocating heap memory via the new operator (see Item 8) and calling strcpy to copy the data in s1 into the memory allocated by s2. This is eager evaluation: making a copy of s1 and putting it into s2 just because the String copy constructor was called. At this point, however, there has been no real need for s2 to have a copy of the value, because s2 hasn't been used yet.

The lazy approach is a lot less work. Instead of giving s2 a copy of s1's value, we have s2 share s1's value. All we have to do is a little bookkeeping so we know who's sharing what, and in return we save the cost of a call to new and the expense of copying anything. The fact that s1 and s2 are sharing a data structure is transparent to clients, and it certainly makes no difference in statements like the following, because they only read values, they don't write them:

In fact, the only time the sharing of values makes a difference is when one or the other string is modified; then it's important that only one string be changed, not both. In this statement,

it's crucial that only s2's value be changed, not s1's also.

To handle statements like this, we have to implement String's convertToUpperCase function so that it makes a copy of s2's value and makes that value private to s2 before modifying it. Inside convertToUpperCase, we can be lazy no longer: we have to make a copy of s2's (shared) value for s2's private use. On the other hand, if s2 is never modified, we never have to make a private copy of its value. It can continue to share a value as long as it exists. If we're lucky, s2 will never be modified, in which case we'll never have to expend the effort to give it its own value.

The details on making this kind of value sharing work (including all the code) are provided in Item 29, but the idea is lazy evaluation: don't bother to make a copy of something until you really need one. Instead, be lazy — use someone else's copy as long as you can get away with it. In some application areas, you can often get away with it forever.

Distinguishing Reads from Writes

Pursuing the example of reference-counting strings a bit further, we come upon a second way in which lazy evaluation can help us. Consider this code:

The first call to operator[] is to read part of a string, but the second call is to perform a write. We'd like to be able to distinguish the read call from the write, because reading a reference-counted string is cheap, but writing to such a string may require splitting off a new copy of the string's value prior to the write.

This puts us in a difficult implementation position. To achieve what we want, we need to do different things inside operator[] (depending on whether it's being called to perform a read or a write). How can we determine whether operator[] has been called in a read or a write context? The brutal truth is that we can't. By using lazy evaluation and proxy classes as described in Item 30, however, we can defer the decision on whether to take read actions or write actions until we can determine which is correct.

Lazy Fetching

As a third example of lazy evaluation, imagine you've got a program that uses large objects containing many constituent fields. Such objects must persist across program runs, so they're stored in a database. Each object has a unique object identifier that can be used to retrieve the object from the database:

Now consider the cost of restoring a LargeObject from disk:

Because LargeObject instances are big, getting all the data for such an object might be a costly database operation, especially if the data must be retrieved from a remote database and pushed across a network. In some cases, the cost of reading all that data would be unnecessary. For example, consider this kind of application:

Here only the value of field2 is required, so any effort spent setting up the other fields is wasted.

The lazy approach to this problem is to read no data from disk when a LargeObject object is created. Instead, only the "shell" of an object is created, and data is retrieved from the database only when that particular data is needed inside the object. Here's one way to implement this kind of "demand-paged" object initialization:

Each field in the object is represented as a pointer to the necessary data, and the LargeObject constructor initializes each pointer to null. Such null pointers signify fields that have not yet been read from the database. Each LargeObject member function must check the state of a field's pointer before accessing the data it points to. If the pointer is null, the corresponding data must be read from the database before performing any operations on that data.

When implementing lazy fetching, you must confront the problem that null pointers may need to be initialized to point to real data from inside any member function, including const member functions like field1. However, compilers get cranky when you try to modify data members inside const member functions, so you've got to find a way to say, "It's okay, I know what I'm doing." The best way to say that is to declare the pointer fields mutable, which means they can be modified inside any member function, even inside const member functions (see Item E21). That's why the fields inside LargeObject above are declared mutable.

The mutable keyword is a relatively recent addition to C++, so it's possible your vendors don't yet support it. If not, you'll need to find another way to convince your compilers to let you modify data members inside const member functions. One workable strategy is the "fake this" approach, whereby you create a pointer-to-non-const that points to the same object as this does. When you want to modify a data member, you access it through the "fake this" pointer:

This function employs a const_cast (see Item 2) to cast away the constness of *this. If your compilers don't support const_cast, you can use an old C-style cast:

Look again at the pointers inside LargeObject. Let's face it, it's tedious and error-prone to have to initialize all those pointers to null, then test each one before use. Fortunately, such drudgery can be automated through the use of smart pointers, which you can read about in Item 28. If you use smart pointers inside LargeObject, you'll also find you no longer need to declare the pointers mutable. Alas, it's only a temporary respite, because you'll wind up needing mutable once you sit down to implement the smart pointer classes. Think of it as conservation of inconvenience.

Lazy Expression Evaluation

A final example of lazy evaluation comes from numerical applications. Consider this code:

The usual implementation of operator+ would use eager evaluation; in this case it would compute and return the sum of m1 and m2. That's a fair amount of computation (1,000,000 additions), and of course there's the cost of allocating the memory to hold all those values, too.

The lazy evaluation strategy says that's way too much work, so it doesn't do it. Instead, it sets up a data structure inside m3 that indicates that m3's value is the sum of m1 and m2. Such a data structure might consist of nothing more than a pointer to each of m1 and m2, plus an enum indicating that the operation on them is addition. Clearly, it's going to be faster to set up this data structure than to add m1 and m2, and it's going to use a lot less memory, too.

Suppose that later in the program, before m3 has been used, this code is executed:

Now we can forget all about m3 being the sum of m1 and m2 (and thereby save the cost of the computation), and in its place we can start remembering that m3 is the product of m4 and m1. Needless to say, we don't perform the multiplication. Why bother? We're lazy, remember?

This example looks contrived, because no good programmer would write a program that computed the sum of two matrices and failed to use it, but it's not as contrived as it seems. No good programmer would deliberately compute a value that's not needed, but during maintenance, it's not uncommon for a programmer to modify the paths through a program in such a way that a formerly useful computation becomes unnecessary. The likelihood of that happening is reduced by defining objects immediately prior to use (see Item E32), but it's still a problem that occurs from time to time.

Nevertheless, if that were the only time lazy evaluation paid off, it would hardly be worth the trouble. A more common scenario is that we need only part of a computation. For example, suppose we use m3 as follows after initializing it to the sum of m1 and m2:

Clearly we can be completely lazy no longer — we've got to compute the values in the fourth row of m3. But let's not be overly ambitious, either. There's no reason we have to compute any more than the fourth row of m3; the remainder of m3 can remain uncomputed until it's actually needed. With luck, it never will be.

How likely are we to be lucky? Experience in the domain of matrix computations suggests the odds are in our favor. In fact, lazy evaluation lies behind the wonder that is APL. APL was developed in the 1960s for interactive use by people who needed to perform matrix-based calculations. Running on computers that had less computational horsepower than the chips now found in high-end microwave ovens, APL was seemingly able to add, multiply, and even divide large matrices instantly! Its trick was lazy evaluation. The trick was usually effective, because APL users typically added, multiplied, or divided matrices not because they needed the entire resulting matrix, but only because they needed a small part of it. APL employed lazy evaluation to defer its computations until it knew exactly what part of a result matrix was needed, then it computed only that part. In practice, this allowed users to perform computationally intensive tasks interactively in an environment where the underlying machine was hopelessly inadequate for an implementation employing eager evaluation. Machines are faster today, but data sets are bigger and users less patient, so many contemporary matrix libraries continue to take advantage of lazy evaluation.

To be fair, laziness sometimes fails to pay off. If m3 is used in this way,

the jig is up and we've got to compute a complete value for m3. Similarly, if one of the matrices on which m3 is dependent is about to be modified, we have to take immediate action:

Here we've got to do something to ensure that the assignment to m1 doesn't change m3. Inside the Matrix<int> assignment operator, we might compute m3's value prior to changing m1 or we might make a copy of the old value of m1 and make m3 dependent on that, but we have to do something to guarantee that m3 has the value it's supposed to have after m1 has been the target of an assignment. Other functions that might modify a matrix must be handled in a similar fashion.

Because of the need to store dependencies between values; to maintain data structures that can store values, dependencies, or a combination of the two; and to overload operators like assignment, copying, and addition, lazy evaluation in a numerical domain is a lot of work. On the other hand, it often ends up saving significant amounts of time and space during program runs, and in many applications, that's a payoff that easily justifies the significant effort lazy evaluation requires.

Summary

These four examples show that lazy evaluation can be useful in a variety of domains: to avoid unnecessary copying of objects, to distinguish reads from writes using operator[], to avoid unnecessary reads from databases, and to avoid unnecessary numerical computations. Nevertheless, it's not always a good idea. Just as procrastinating on your clean-up chores won't save you any work if your parents always check up on you, lazy evaluation won't save your program any work if all your computations are necessary. Indeed, if all your computations are essential, lazy evaluation may slow you down and increase your use of memory, because, in addition to having to do all the computations you were hoping to avoid, you'll also have to manipulate the fancy data structures needed to make lazy evaluation possible in the first place. Lazy evaluation is only useful when there's a reasonable chance your software will be asked to perform computations that can be avoided.

There's nothing about lazy evaluation that's specific to C++. The technique can be applied in any programming language, and several languages — notably APL, some dialects of Lisp, and virtually all dataflow languages — embrace the idea as a fundamental part of the language. Mainstream programming languages employ eager evaluation, however, and C++ is mainstream. Yet C++ is particularly suitable as a vehicle for user-implemented lazy evaluation, because its support for encapsulation makes it possible to add lazy evaluation to a class without clients of that class knowing it's been done.

Look again at the code fragments used in the above examples, and you can verify that the class interfaces offer no hints about whether eager or lazy evaluation is used by the classes. That means it's possible to implement a class using a straightforward eager evaluation strategy, but then, if your profiling investigations (see Item 16) show that class's implementation is a performance bottleneck, you can replace its implementation with one based on lazy evaluation. (See also Item E34.) The only change your clients will see (after recompilation or relinking) is improved performance. That's the kind of software enhancement clients love, one that can make you downright proud to be lazy.

Back to Item 17: Consider using lazy evaluation   
  Continue to Item 19: Understand the origin of temporary objects

Item 18:  Amortize the cost of expected computations.

In Item 17, I extolled the virtues of laziness, of putting things off as long as possible, and I explained how laziness can improve the efficiency of your programs. In this item, I adopt a different stance. Here, laziness has no place. I now encourage you to improve the performance of your software by having it do more than it's asked to do. The philosophy of this item might be called over-eager evaluation: doing things before you're asked to do them.

Consider, for example, a template for classes representing large collections of numeric data:

Assuming the min, max, and avg functions return the current minimum, maximum, and average values of the collection, there are three ways in which these functions can be implemented. Using eager evaluation, we'd examine all the data in the collection when min, max, or avg was called, and we'd return the appropriate value. Using lazy evaluation, we'd have the functions return data structures that could be used to determine the appropriate value whenever the functions' return values were actually used. Using over-eager evaluation, we'd keep track of the running minimum, maximum, and average values of the collection, so when min, max, or avg was called, we'd be able to return the correct value immediately — no computation would be required. If min, max, and avg were called frequently, we'd be able to amortize the cost of keeping track of the collection's minimum, maximum, and average values over all the calls to those functions, and the amortized cost per call would be lower than with eager or lazy evaluation.

The idea behind over-eager evaluation is that if you expect a computation to be requested frequently, you can lower the average cost per request by designing your data structures to handle the requests especially efficiently.

One of the simplest ways to do this is by caching values that have already been computed and are likely to be needed again. For example, suppose you're writing a program to provide information about employees, and one of the pieces of information you expect to be requested frequently is an employee's cubicle number. Further suppose that employee information is stored in a database, but, for most applications, an employee's cubicle number is irrelevant, so the database is not optimized to find it. To avoid having your specialized application unduly stress the database with repeated lookups of employee cubicle numbers, you could write a findCubicleNumber function that caches the cubicle numbers it looks up. Subsequent requests for cubicle numbers that have already been retrieved can then be satisfied by consulting the cache instead of querying the database.

Here's one way to implement findCubicleNumber; it uses a map object from the Standard Template Library (the "STL" — see Item 35) as a local cache:

Try not to get bogged down in the details of the STL code (which will be clearer after you've read Item 35). Instead, focus on the general strategy embodied by this function. That strategy is to use a local cache to replace comparatively expensive database queries with comparatively inexpensive lookups in an in-memory data structure. Provided we're correct in assuming that cubicle numbers will frequently be requested more than once, the use of a cache in findCubicleNumber should reduce the average cost of returning an employee's cubicle number.

(One detail of the code requires explanation. The final statement returns (*it).second instead of the more conventional it->second. Why? The answer has to do with the conventions followed by the STL. In brief, the iterator it is an object, not a pointer, so there is no guarantee that "->" can be applied to it.6 The STL does require that "." and "*" be valid for iterators, however, so (*it).second, though syntactically clumsy, is guaranteed to work.)

Caching is one way to amortize the cost of anticipated computations. Prefetching is another. You can think of prefetching as the computational equivalent of a discount for buying in bulk. Disk controllers, for example, read entire blocks or sectors of data when they read from disk, even if a program asks for only a small amount of data. That's because it's faster to read a big chunk once than to read two or three small chunks at different times. Furthermore, experience has shown that if data in one place is requested, it's quite common to want nearby data, too. This is the infamous locality of reference phenomenon, and systems designers rely on it to justify disk caches, memory caches for both instructions and data, and instruction prefetches.

Excuse me? You say you don't worry about such low-level things as disk controllers or CPU caches? No problem. Prefetching can yield dividends for even one as high-level as you. Imagine, for example, you'd like to implement a template for dynamic arrays, i.e., arrays that start with a size of one and automatically extend themselves so that all nonnegative indices are valid:

How does a DynArray object go about extending itself when it needs to? A straightforward strategy would be to allocate only as much additional memory as needed, something like this:

This approach simply calls new each time it needs to increase the size of the array, but calls to new invoke operator new (see Item 8), and calls to operator new (and operator delete) are usually expensive. That's because they typically result in calls to the underlying operating system, and system calls are generally slower than are in-process function calls. As a result, we'd like to make as few system calls as possible.

An over-eager evaluation strategy employs this reasoning: if we have to increase the size of the array now to accommodate index i, the locality of reference principle suggests we'll probably have to increase it in the future to accommodate some other index a bit larger than i. To avoid the cost of the memory allocation for the second (anticipated) expansion, we'll increase the size of the DynArray now by more than is required to make i valid, and we'll hope that future expansions occur within the range we have thereby provided for. For example, we could write DynArray::operator[] like this:

This function allocates twice as much memory as needed each time the array must be extended. If we look again at the usage scenario we saw earlier, we note that the DynArray must allocate additional memory only once, even though its logical size is extended twice:

If a needs to be extended again, that extension, too, will be inexpensive, provided the new maximum index is no greater than 44.

There is a common theme running through this Item, and that's that greater speed can often be purchased at a cost of increased memory usage. Keeping track of running minima, maxima, and averages requires extra space, but it saves time. Caching results necessitates greater memory usage but reduces the time needed to regenerate the results once they've been cached. Prefetching demands a place to put the things that are prefetched, but it reduces the time needed to access those things. The story is as old as Computer Science: you can often trade space for time. (Not always, however. Using larger objects means fewer fit on a virtual memory or cache page. In rare cases, making objects bigger reduces the performance of your software, because your paging activity increases, your cache hit rate decreases, or both. How do you find out if you're suffering from such problems? You profile, profile, profile (see Item 16).)

The advice I proffer in this Item — that you amortize the cost of anticipated computations through over-eager strategies like caching and prefetching — is not contradictory to the advice on lazy evaluation I put forth in Item 17. Lazy evaluation is a technique for improving the efficiency of programs when you must support operations whose results are not always needed. Over-eager evaluation is a technique for improving the efficiency of programs when you must support operations whose results are almost always needed or whose results are often needed more than once. Both are more difficult to implement than run-of-the-mill eager evaluation, but both can yield significant performance improvements in programs whose behavioral characteristics justify the extra programming effort.

Back to Item 18: Amortize the cost of expected computations   
  Continue to Item 20: Facilitate the return value optimization

Item 19:  Understand the origin of temporary objects.

When programmers speak amongst themselves, they often refer to variables that are needed for only a short while as "temporaries." For example, in this swap routine,

it's common to call temp a "temporary." As far as C++ is concerned, however, temp is not a temporary at all. It's simply an object local to a function.

True temporary objects in C++ are invisible — they don't appear in your source code. They arise whenever a non-heap object is created but not named. Such unnamed objects usually arise in one of two situations: when implicit type conversions are applied to make function calls succeed and when functions return objects. It's important to understand how and why these temporary objects are created and destroyed, because the attendant costs of their construction and destruction can have a noticeable impact on the performance of your programs.

Consider first the case in which temporary objects are created to make function calls succeed. This happens when the type of object passed to a function is not the same as the type of the parameter to which it is being bound. For example, consider a function that counts the number of occurrences of a character in a string:

Look at the call to countChar. The first argument passed is a char array, but the corresponding function parameter is of type const string&. This call can succeed only if the type mismatch can be eliminated, and your compilers will be happy to eliminate it by creating a temporary object of type string. That temporary object is initialized by calling the string constructor with buffer as its argument. The str parameter of countChar is then bound to this temporary string object. When countChar returns, the temporary object is automatically destroyed.

Conversions such as these are convenient (though dangerous — see Item 5), but from an efficiency point of view, the construction and destruction of a temporary string object is an unnecessary expense. There are two general ways to eliminate it. One is to redesign your code so conversions like these can't take place. That strategy is examined in Item 5. An alternative tack is to modify your software so that the conversions are unnecessary. Item 21 describes how you can do that.

These conversions occur only when passing objects by value or when passing to a reference-to-const parameter. They do not occur when passing an object to a reference-to-non-const parameter. Consider this function:

In the character-counting example, a char array could be successfully passed to countChar, but here, trying to call uppercasify with a char array fails:

No temporary is created to make the call succeed. Why not?

Suppose a temporary were created. Then the temporary would be passed to uppercasify, which would modify the temporary so its characters were in upper case. But the actual argument to the function call — subtleBookPlug — would not be affected; only the temporary string object generated from subtleBookPlug would be changed. Surely this is not what the programmer intended. That programmer passed subtleBookPlug to uppercasify, and that programmer expected subtleBookPlug to be modified. Implicit type conversion for references-to-non-const objects, then, would allow temporary objects to be changed when programmers expected non-temporary objects to be modified. That's why the language prohibits the generation of temporaries for non-const reference parameters. Reference-to-const parameters don't suffer from this problem, because such parameters, by virtue of being const, can't be changed.

The second set of circumstances under which temporary objects are created is when a function returns an object. For instance, operator+ must return an object that represents the sum of its operands (see Item E23). Given a type Number, for example, operator+ for that type would be declared like this:

The return value of this function is a temporary, because it has no name: it's just the function's return value. You must pay to construct and destruct this object each time you call operator+. (For an explanation of why the return value is const, see Item E21.)

As usual, you don't want to incur this cost. For this particular function, you can avoid paying by switching to a similar function, operator+=; Item 22 tells you about this transformation. For most functions that return objects, however, switching to a different function is not an option and there is no way to avoid the construction and destruction of the return value. At least, there's no way to avoid it conceptually. Between concept and reality, however, lies a murky zone called optimization, and sometimes you can write your object-returning functions in a way that allows your compilers to optimize temporary objects out of existence. Of these optimizations, the most common and useful is the return value optimization, which is the subject of Item 20.

The bottom line is that temporary objects can be costly, so you want to eliminate them whenever you can. More important than this, however, is to train yourself to look for places where temporary objects may be created. Anytime you see a reference-to-const parameter, the possibility exists that a temporary will be created to bind to that parameter. Anytime you see a function returning an object, a temporary will be created (and later destroyed). Learn to look for such constructs, and your insight into the cost of "behind the scenes" compiler actions will markedly improve.

Back to Item 19: Understand the origin of temporary objects   
  Continue to Item 21: Overload to avoid implicit type conversions

Item 20:  Facilitate the return value optimization.

A function that returns an object is frustrating to efficiency aficionados, because the by-value return, including the constructor and destructor calls it implies (see Item 19), cannot be eliminated. The problem is simple: a function either has to return an object in order to offer correct behavior or it doesn't. If it does, there's no way to get rid of the object being returned. Period.

Consider the operator* function for rational numbers:

Without even looking at the code for operator*, we know it must return an object, because it returns the product of two arbitrary numbers. These are arbitrary numbers. How can operator* possibly avoid creating a new object to hold their product? It can't, so it must create a new object and return it. C++ programmers have nevertheless expended Herculean efforts in a search for the legendary elimination of the by-value return (see Items E23 and E31).

Sometimes people return pointers, which leads to this syntactic travesty:

It also raises a question. Should the caller delete the pointer returned by the function? The answer is usually yes, and that usually leads to resource leaks.

Other developers return references. That yields an acceptable syntax,

but such functions can't be implemented in a way that behaves correctly. A common attempt looks like this:

This function returns a reference to an object that no longer exists. In particular, it returns a reference to the local object result, but result is automatically destroyed when operator* is exited. Returning a reference to an object that's been destroyed is hardly useful.

Trust me on this: some functions (operator* among them) just have to return objects. That's the way it is. Don't fight it. You can't win.

That is, you can't win in your effort to eliminate by-value returns from functions that require them. But that's the wrong war to wage. From an efficiency point of view, you shouldn't care that a function returns an object, you should only care about the cost of that object. What you need to do is channel your efforts into finding a way to reduce the cost of returned objects, not to eliminate the objects themselves (which we now recognize is a futile quest). If no cost is associated with such objects, who cares how many get created?

It is frequently possible to write functions that return objects in such a way that compilers can eliminate the cost of the temporaries. The trick is to return constructor arguments instead of objects, and you can do it like this:

Look closely at the expression being returned. It looks like you're calling a Rational constructor, and in fact you are. You're creating a temporary Rational object through this expression,

and it is this temporary object the function is copying for its return value.

This business of returning constructor arguments instead of local objects doesn't appear to have bought you a lot, because you still have to pay for the construction and destruction of the temporary created inside the function, and you still have to pay for the construction and destruction of the object the function returns. But you have gained something. The rules for C++ allow compilers to optimize temporary objects out of existence. As a result, if you call operator* in a context like this,

your compilers are allowed to eliminate both the temporary inside operator* and the temporary returned by operator*. They can construct the object defined by the return expression inside the memory allotted for the object c. If your compilers do this, the total cost of temporary objects as a result of your calling operator* is zero: no temporaries are created. Instead, you pay for only one constructor call — the one to create c. Furthermore, you can't do any better than this, because c is a named object, and named objects can't be eliminated (see also Item 22).7 You can, however, eliminate the overhead of the call to operator* by declaring that function inline (but first see Item E33):

"Yeah, yeah," you mutter, "optimization, schmoptimization. Who cares what compilers can do? I want to know what they do do. Does any of this nonsense work with real compilers?" It does. This particular optimization — eliminating a local temporary by using a function's return location (and possibly replacing that with an object at the function's call site) — is both well-known and commonly implemented. It even has a name: the return value optimization. In fact, the existence of a name for this optimization may explain why it's so widely available. Programmers looking for a C++ compiler can ask vendors whether the return value optimization is implemented. If one vendor says yes and another says "The what?," the first vendor has a notable competitive advantage. Ah, capitalism. Sometimes you just gotta love it.

Back to Item 20: Facilitate the return value optimization   
  Continue to Item 22: Consider using op= instead of stand-alone op

Item 21:  Overload to avoid implicit type conversions.

Here's some code that looks nothing if not eminently reasonable:

There are no surprises here. upi1 and upi2 are both UPInt objects, so adding them together just calls operator+ for UPInts.

Now consider these statements:

These statements also succeed. They do so through the creation of temporary objects to convert the integer 10 into UPInts (see Item 19).

It is convenient to have compilers perform these kinds of conversions, but the temporary objects created to make the conversions work are a cost we may not wish to bear. Just as most people want government benefits without having to pay for them, most C++ programmers want implicit type conversions without incurring any cost for temporaries. But without the computational equivalent of deficit spending, how can we do it?

We can take a step back and recognize that our goal isn't really type conversion, it's being able to make calls to operator+ with a combination of UPInt and int arguments. Implicit type conversion happens to be a means to that end, but let us not confuse means and ends. There is another way to make mixed-type calls to operator+ succeed, and that's to eliminate the need for type conversions in the first place. If we want to be able to add UPInt and int objects, all we have to do is say so. We do it by declaring several functions, each with a different set of parameter types:

Once you start overloading to eliminate type conversions, you run the risk of getting swept up in the passion of the moment and declaring functions like this:

The thinking here is reasonable enough. For the types UPInt and int, we want to overload on all possible combinations for operator+. Given the three overloadings above, the only one missing is operator+ taking two int arguments, so we want to add it.

Reasonable or not, there are rules to this C++ game, and one of them is that every overloaded operator must take at least one argument of a user-defined type. int isn't a user-defined type, so we can't overload an operator taking only arguments of that type. (If this rule didn't exist, programmers would be able to change the meaning of predefined operations, and that would surely lead to chaos. For example, the attempted overloading of operator+ above would change the meaning of addition on ints. Is that really something we want people to be able to do?)

Overloading to avoid temporaries isn't limited to operator functions. For example, in most programs, you'll want to allow a string object everywhere a char* is acceptable, and vice versa. Similarly, if you're using a numerical class like complex (see Item 35), you'll want types like int and double to be valid anywhere a numerical object is. As a result, any function taking arguments of type string, char*, complex, etc., is a reasonable candidate for overloading to eliminate type conversions.

Still, it's important to keep the 80-20 rule (see Item 16) in mind. There is no point in implementing a slew of overloaded functions unless you have good reason to believe that it will make a noticeable improvement in the overall efficiency of the programs that use them.

Back to Item 21: Overload to avoid implicit type conversions   
  Continue to Item 23: Consider alternative libraries

Item 22:  Consider using op= instead of stand-alone op.

Most programmers expect that if they can say things like these,

they can also say things like these:

If x and y are of a user-defined type, there is no guarantee that this is so. As far as C++ is concerned, there is no relationship between operator+, operator=, and operator+=, so if you want all three operators to exist and to have the expected relationship, you must implement that yourself. Ditto for the operators -, *, /, etc.

A good way to ensure that the natural relationship between the assignment version of an operator (e.g., operator+=) and the stand-alone version (e.g., operator+) exists is to implement the latter in terms of the former (see also Item 6). This is easy to do:

In this example, operators += and -= are implemented (elsewhere) from scratch, and operator+ and operator- call them to provide their own functionality. With this design, only the assignment versions of these operators need to be maintained. Furthermore, assuming the assignment versions of the operators are in the class's public interface, there is never a need for the stand-alone operators to be friends of the class (see Item E19).

If you don't mind putting all stand-alone operators at global scope, you can use templates to eliminate the need to write the stand-alone functions:

With these templates, as long as an assignment version of an operator is defined for some type T, the corresponding stand-alone operator will automatically be generated if it's needed.

All this is well and good, but so far we have failed to consider the issue of efficiency, and efficiency is, after all, the topic of this chapter. Three aspects of efficiency are worth noting here. The first is that, in general, assignment versions of operators are more efficient than stand-alone versions, because stand-alone versions must typically return a new object, and that costs us the construction and destruction of a temporary (see Items 19 and 20, as well as Item E23). Assignment versions of operators write to their left-hand argument, so there is no need to generate a temporary to hold the operator's return value.

The second point is that by offering assignment versions of operators as well as stand-alone versions, you allow clients of your classes to make the difficult trade-off between efficiency and convenience. That is, your clients can decide whether to write their code like this,

or like this:

The former is easier to write, debug, and maintain, and it offers acceptable performance about 80% of the time (see Item 16). The latter is more efficient, and, one supposes, more intuitive for assembly language programmers. By offering both options, you let clients develop and debug code using the easier-to-read stand-alone operators while still reserving the right to replace them with the more efficient assignment versions of the operators. Furthermore, by implementing the stand-alones in terms of the assignment versions, you ensure that when clients switch from one to the other, the semantics of the operations remain constant.

The final efficiency observation concerns implementing the stand-alone operators. Look again at the implementation for operator+:

The expression T(lhs) is a call to T's copy constructor. It creates a temporary object whose value is the same as that of lhs. This temporary is then used to invoke operator+= with rhs, and the result of that operation is returned from operator+.8 This code seems unnecessarily cryptic. Wouldn't it be better to write it like this?

This template is almost equivalent to the one above, but there is a crucial difference. This second template contains a named object, result. The fact that this object is named means that the return value optimization (see Item 20) was, until relatively recently, unavailable for this implementation of operator+ (see the footnote on page 104). The first implementation has always been eligible for the return value optimization, so the odds may be better that the compilers you use will generate optimized code for it.

Now, truth in advertising compels me to point out that the expression

is more complex than most compilers are willing to subject to the return value optimization. The first implementation above may thus cost you one temporary object within the function, just as you'd pay for using the named object result. However, the fact remains that unnamed objects have historically been easier to eliminate than named objects, so when faced with a choice between a named object and a temporary object, you may be better off using the temporary. It should never cost you more than its named colleague, and, especially with older compilers, it may cost you less.

All this talk of named objects, unnamed objects, and compiler optimizations is interesting, but let us not forget the big picture. The big picture is that assignment versions of operators (such as operator+=) tend to be more efficient than stand-alone versions of those operators (e.g. operator+). As a library designer, you should offer both, and as an application developer, you should consider using assignment versions of operators instead of stand-alone versions whenever performance is at a premium.

Back to Item 22: Consider using op= instead of stand-alone op   
  Continue to Item 24: Understand the costs of virtual functions, multiple inheritance, virtual base classes, and RTTI

Item 23:  Consider alternative libraries.

Library design is an exercise in compromise. The ideal library is small, fast, powerful, flexible, extensible, intuitive, universally available, well supported, free of use restrictions, and bug-free. It is also nonexistent. Libraries optimized for size and speed are typically not portable. Libraries with rich functionality are rarely intuitive. Bug-free libraries are limited in scope. In the real world, you can't have everything; something always has to give.

Different designers assign different priorities to these criteria. They thus sacrifice different things in their designs. As a result, it is not uncommon for two libraries offering similar functionality to have quite different performance profiles.

As an example, consider the iostream and stdio libraries, both of which should be available to every C++ programmer. The iostream library has several advantages over its C counterpart (see Item E2). It's type-safe, for example, and it's extensible. In terms of efficiency, however, the iostream library generally suffers in comparison with stdio, because stdio usually results in executables that are both smaller and faster than those arising from iostreams.

Consider first the speed issue. One way to get a feel for the difference in performance between iostreams and stdio is to run benchmark applications using both libraries. Now, it's important to bear in mind that benchmarks lie. Not only is it difficult to come up with a set of inputs that correspond to "typical" usage of a program or library, it's also useless unless you have a reliable way of determining how "typical" you or your clients are. Nevertheless, benchmarks can provide some insight into the comparative performance of different approaches to a problem, so though it would be foolish to rely on them completely, it would also be foolish to ignore them.

Let's examine a simple-minded benchmark program that exercises only the most rudimentary I/O functionality. This program reads 30,000 floating point numbers from standard input and writes them to standard output in a fixed format. The choice between the iostream and stdio libraries is made during compilation and is determined by the preprocessor symbol STDIO. If this symbol is defined, the stdio library is used, otherwise the iostream library is employed.

When this program is given the natural logarithms of the positive integers as input, it produces output like this:

Such output demonstrates, if nothing else, that it's possible to produce fixed-format I/O using iostreams. Of course,

is nowhere near as easy to type as

but operator<< is both type-safe and extensible, and printf is neither.

I have run this program on several combinations of machines, operating systems, and compilers, and in every case the stdio version has been faster. Sometimes it's been only a little faster (about 20%), sometimes it's been substantially faster (nearly 200%), but I've never come across an iostream implementation that was as fast as the corresponding stdio implementation. In addition, the size of this trivial program's executable using stdio tends to be smaller (sometimes much smaller) than the corresponding program using iostreams. (For programs of a realistic size, this difference is rarely significant.)

Bear in mind that any efficiency advantages of stdio are highly implementation-dependent, so future implementations of systems I've tested or existing implementations of systems I haven't tested may show a negligible performance difference between iostreams and stdio. In fact, one can reasonably hope to discover an iostream implementation that's faster than stdio, because iostreams determine the types of their operands during compilation, while stdio functions typically parse a format string at runtime.

The contrast in performance between iostreams and stdio is just an example, however, it's not the main point. The main point is that different libraries offering similar functionality often feature different performance trade-offs, so once you've identified the bottlenecks in your software (via profiling — see Item 16), you should see if it's possible to remove those bottlenecks by replacing one library with another. If your program has an I/O bottleneck, for example, you might consider replacing iostreams with stdio, but if it spends a significant portion of its time on dynamic memory allocation and deallocation, you might see if there are alternative implementations of operator new and operator delete available (see Item 8 and Item E10). Because different libraries embody different design decisions regarding efficiency, extensibility, portability, type safety, and other issues, you can sometimes significantly improve the efficiency of your software by switching to libraries whose designers gave more weight to performance considerations than to other factors.

Back to Item 23: Consider alternative libraries   
  Continue to Techniques

Item 24:  Understand the costs of virtual functions, multiple inheritance, virtual base classes, and RTTI.

C++ compilers must find a way to implement each feature in the language. Such implementation details are, of course, compiler-dependent, and different compilers implement language features in different ways. For the most part, you need not concern yourself with such matters. However, the implementation of some features can have a noticeable impact on the size of objects and the speed at which member functions execute, so for those features, it's important to have a basic understanding of what compilers are likely to be doing under the hood. The foremost example of such a feature is virtual functions.

When a virtual function is called, the code executed must correspond to the dynamic type of the object on which the function is invoked; the type of the pointer or reference to the object is immaterial. How can compilers provide this behavior efficiently? Most implementations use virtual tables and virtual table pointers. Virtual tables and virtual table pointers are commonly referred to as vtbls and vptrs, respectively.

A vtbl is usually an array of pointers to functions. (Some compilers use a form of linked list instead of an array, but the fundamental strategy is the same.) Each class in a program that declares or inherits virtual functions has its own vtbl, and the entries in a class's vtbl are pointers to the implementations of the virtual functions for that class. For example, given a class definition like this,

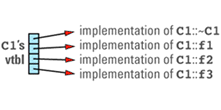
C1's virtual table array will look something like this:

Note that the nonvirtual function f4 is not in the table, nor is C1's constructor. Nonvirtual functions — including constructors, which are by definition nonvirtual — are implemented just like ordinary C functions, so there are no special performance considerations surrounding their use.

If a class C2 inherits from C1, redefines some of the virtual functions it inherits, and adds some new ones of its own,

its virtual table entries point to the functions that are appropriate for objects of its type. These entries include pointers to the C1 virtual functions that C2 chose not to redefine:

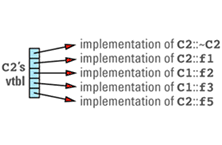
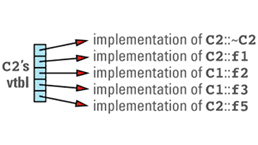
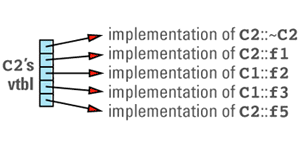
This discussion brings out the first cost of virtual functions: you have to set aside space for a virtual table for each class that contains virtual functions. The size of a class's vtbl is proportional to the number of virtual functions declared for that class (including those it inherits from its base classes). There should be only one virtual table per class, so the total amount of space required for virtual tables is not usually significant, but if you have a large number of classes or a large number of virtual functions in each class, you may find that the vtbls take a significant bite out of your address space.

Because you need only one copy of a class's vtbl in your programs, compilers must address a tricky problem: where to put it. Most programs and libraries are created by linking together many object files, but each object file is generated independently of the others. Which object file should contain the vtbl for any given class? You might think to put it in the object file containing main, but libraries have no main, and at any rate the source file containing main may make no mention of many of the classes requiring vtbls. How could compilers then know which vtbls they were supposed to create?

A different strategy must be adopted, and compiler vendors tend to fall into two camps. For vendors who provide an integrated environment containing both compiler and linker, a brute-force strategy is to generate a copy of the vtbl in each object file that might need it. The linker then strips out duplicate copies, leaving only a single instance of each vtbl in the final executable or library.

A more common design is to employ a heuristic to determine which object file should contain the vtbl for a class. Usually this heuristic is as follows: a class's vtbl is generated in the object file containing the definition (i.e., the body) of the first non-inline non-pure virtual function in that class. Thus, the vtbl for class C1 above would be placed in the object file containing the definition of C1::~C1 (provided that function wasn't inline), and the vtbl for class C2 would be placed in the object file containing the definition of C2::~C2 (again, provided that function wasn't inline).

In practice, this heuristic works well, but you can get into trouble if you go overboard on declaring virtual functions inline (see Item E33). If all virtual functions in a class are declared inline, the heuristic fails, and most heuristic-based implementations then generate a copy of the class's vtbl in every object file that uses it. In large systems, this can lead to programs containing hundreds or thousands of copies of a class's vtbl! Most compilers following this heuristic give you some way to control vtbl generation manually, but a better solution to this problem is to avoid declaring virtual functions inline. As we'll see below, there are good reasons why present compilers typically ignore the inline directive for virtual functions, anyway.

Virtual tables are half the implementation machinery for virtual functions, but by themselves they are useless. They become useful only when there is some way of indicating which vtbl corresponds to each object, and it is the job of the virtual table pointer to establish that correspondence.

Each object whose class declares virtual functions carries with it a hidden data member that points to the virtual table for that class. This hidden data member — the vptr — is added by compilers at a location in the object known only to the compilers. Conceptually, we can think of the layout of an object that has virtual functions as looking like this:

This picture shows the vptr at the end of the object, but don't be fooled: different compilers put them in different places. In the presence of inheritance, an object's vptr is often surrounded by data members. Multiple inheritance complicates this picture, but we'll deal with that a bit later. At this point, simply note the second cost of virtual functions: you have to pay for an extra pointer inside each object that is of a class containing virtual functions.

If your objects are small, this can be a significant cost. If your objects contain, on average, four bytes of member data, for example, the addition of a vptr can double their size (assuming four bytes are devoted to the vptr). On systems with limited memory, this means the number of objects you can create is reduced. Even on systems with unconstrained memory, you may find that the performance of your software decreases, because larger objects mean fewer fit on each cache or virtual memory page, and that means your paging activity will probably increase.

Suppose we have a program with several objects of types C1 and C2. Given the relationships among objects, vptrs, and vtbls that we have just seen, we can envision the objects in our program like this:

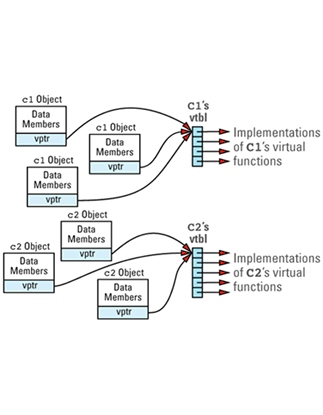
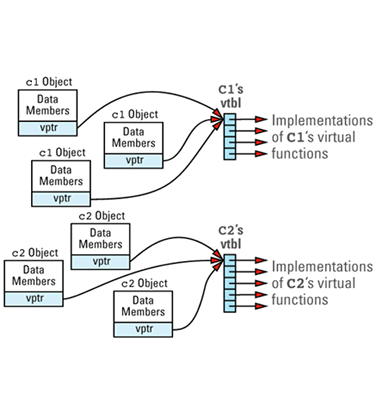
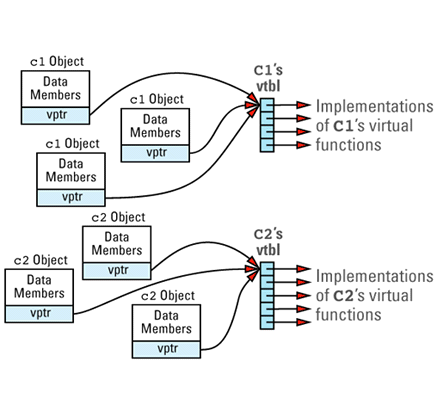
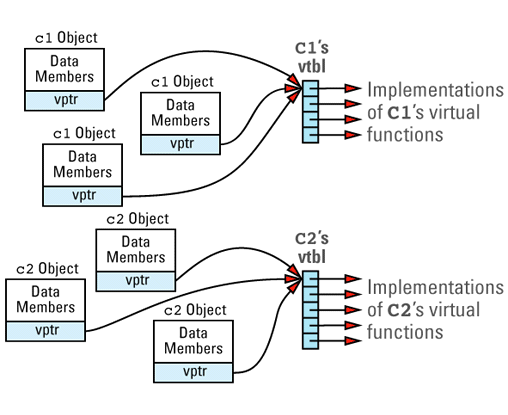
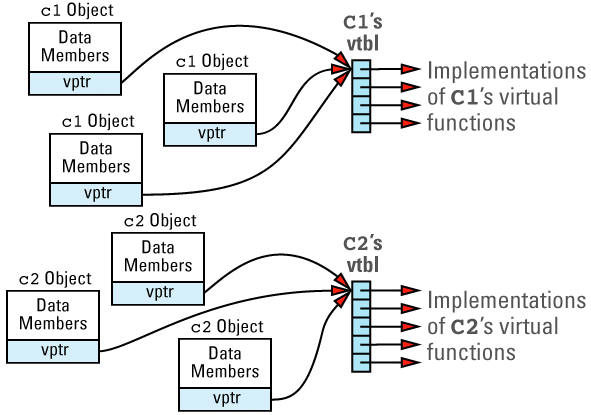
Now consider this program fragment:

This is a call to the virtual function f1 through the pointer pC1. By looking only at this code, there is no way to know which f1 function — C1::f1 or C2::f1 — should be invoked, because pC1 might point to a C1 object or to a C2 object. Your compilers must nevertheless generate code for the call to f1 inside makeACall, and they must ensure that the correct function is called, no matter what pC1 points to. They do this by generating code to do the following:

  1. Follow the object's vptr to its vtbl. This is a simple operation, because the compilers know where to look inside the object for the vptr. (After all, they put it there.) As a result, this costs only an offset adjustment (to get to the vptr) and a pointer indirection (to get to the vtbl).
  2. Find the pointer in the vtbl that corresponds to the function being called (f1 in this example). This, too, is simple, because compilers assign each virtual function a unique index within the table. The cost of this step is just an offset into the vtbl array.
  3. Invoke the function pointed to by the pointer located in step 2.

If we imagine that each object has a hidden member called vptr and that the vtbl index of function f1 is i, the code generated for the statement

is

This is almost as efficient as a non-virtual function call: on most machines it executes only a few more instructions. The cost of calling a virtual function is thus basically the same as that of calling a function through a function pointer. Virtual functions per se are not usually a performance bottleneck.

The real runtime cost of virtual functions has to do with their interaction with inlining. For all practical purposes, virtual functions aren't inlined. That's because "inline" means "during compilation, replace the call site with the body of the called function," but "virtual" means "wait until runtime to see which function is called." If your compilers don't know which function will be called at a particular call site, you can understand why they won't inline that function call. This is the third cost of virtual functions: you effectively give up inlining. (Virtual functions can be inlined when invoked through objects, but most virtual function calls are made through pointers or references to objects, and such calls are not inlined. Because such calls are the norm, virtual functions are effectively not inlined.)

Everything we've seen so far applies to both single and multiple inheritance, but when multiple inheritance enters the picture, things get more complex (see Item E43). There is no point in dwelling on details, but with multiple inheritance, offset calculations to find vptrs within objects become more complicated; there are multiple vptrs within a single object (one per base class); and special vtbls must be generated for base classes in addition to the stand-alone vtbls we have discussed. As a result, both the per-class and the per-object space overhead for virtual functions increases, and the runtime invocation cost grows slightly, too.

Multiple inheritance often leads to the need for virtual base classes. Without virtual base classes, if a derived class has more than one inheritance path to a base class, the data members of that base class are replicated within each derived class object, one copy for each path between the derived class and the base class. Such replication is almost never what programmers want, and making base classes virtual eliminates the replication. Virtual base classes may incur a cost of their own, however, because implementations of virtual base classes often use pointers to virtual base class parts as the means for avoiding the replication, and one or more of those pointers may be stored inside your objects.

For example, consider this, which I generally call "the dreaded multiple inheritance diamond:"

Here A is a virtual base class because B and C virtually inherit from it. With some compilers (especially older compilers), the layout for an object of type D is likely to look like this:

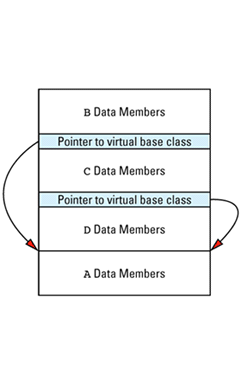
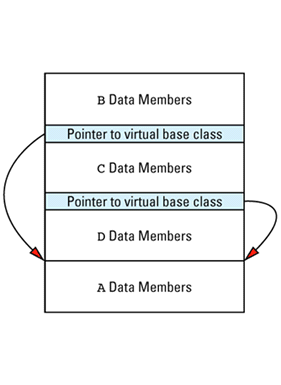
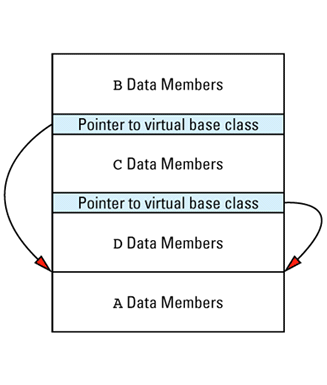
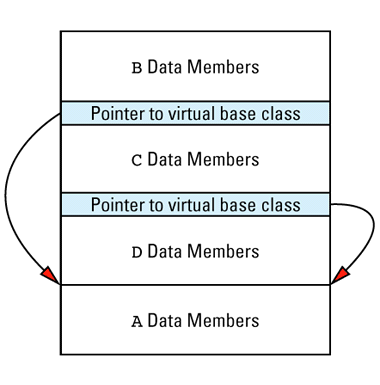
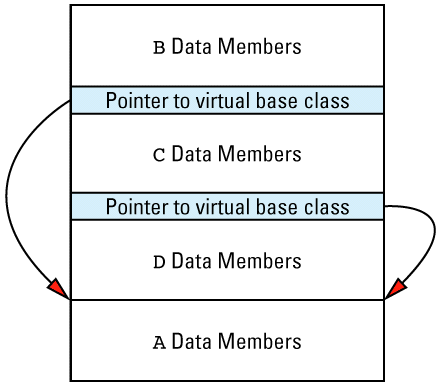
It seems a little strange to place the base class data members at the end of the object, but that's often how it's done. Of course, implementations are free to organize memory any way they like, so you should never rely on this picture for anything more than a conceptual overview of how virtual base classes may lead to the addition of hidden pointers to your objects. Some implementations add fewer pointers, and some find ways to add none at all. (Such implementations make the vptr and vtbl serve double duty).

If we combine this picture with the earlier one showing how virtual table pointers are added to objects, we realize that if the base class A in the hierarchy on page 119 has any virtual functions, the memory layout for an object of type D could look like this:

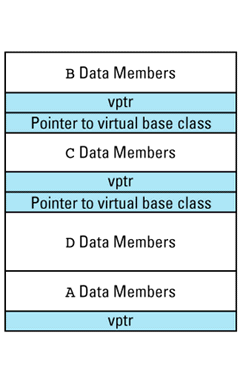
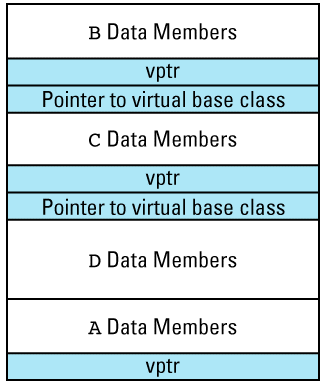
Here I've shaded the parts of the object that are added by compilers. The picture may be misleading, because the ratio of shaded to unshaded areas is determined by the amount of data in your classes. For small classes, the relative overhead is large. For classes with more data, the relative overhead is less significant, though it is typically noticeable.

An oddity in the above diagram is that there are only three vptrs even though four classes are involved. Implementations are free to generate four vptrs if they like, but three suffice (it turns out that B and D can share a vptr), and most implementations take advantage of this opportunity to reduce the compiler-generated overhead.

We've now seen how virtual functions make objects larger and preclude inlining, and we've examined how multiple inheritance and virtual base classes can also increase the size of objects. Let us therefore turn to our final topic, the cost of runtime type identification (RTTI).

RTTI lets us discover information about objects and classes at runtime, so there has to be a place to store the information we're allowed to query. That information is stored in an object of type type_info, and you can access the type_info object for a class by using the typeid operator.

There only needs to be a single copy of the RTTI information for each class, but there must be a way to get to that information for any object. Actually, that's not quite true. The language specification states that we're guaranteed accurate information on an object's dynamic type only if that type has at least one virtual function. This makes RTTI data sound a lot like a virtual function table. We need only one copy of the information per class, and we need a way to get to the appropriate information from any object containing a virtual function. This parallel between RTTI and virtual function tables is no accident: RTTI was designed to be implementable in terms of a class's vtbl.

For example, index 0 of a vtbl array might contain a pointer to the type_info object for the class corresponding to that vtbl. The vtbl for class C1 on page 114 would then look like this:

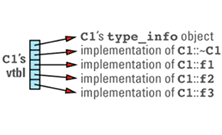
With this implementation, the space cost of RTTI is an additional entry in each class vtbl plus the cost of the storage for the type_info object for each class. Just as the memory for virtual tables is unlikely to be noticeable for most applications, however, you're unlikely to run into problems due to the size of type_info objects.

The following table summarizes the primary costs of virtual functions, multiple inheritance, virtual base classes, and RTTI:

Feature Increases
Size of Objects		 Increases
Per-Class Data		 Reduces
Inlining
Virtual FunctionsYesYesYes
Multiple InheritanceYesYesNo
Virtual Base ClassesOftenSometimesNo
RTTINoYesNo

Some people look at this table and are aghast. "I'm sticking with C!", they declare. Fair enough. But remember that each of these features offers functionality you'd otherwise have to code by hand. In most cases, your manual approximation would probably be less efficient and less robust than the compiler-generated code. Using nested switch statements or cascading if-then-elses to emulate virtual function calls, for example, yields more code than virtual function calls do, and the code runs more slowly, too. Furthermore, you must manually track object types yourself, which means your objects carry around type tags of their own; you thus often fail to gain even the benefit of smaller objects.

It is important to understand the costs of virtual functions, multiple inheritance, virtual base classes, and RTTI, but it is equally important to understand that if you need the functionality these features offer, you will pay for it, one way or another. Sometimes you have legitimate reasons for bypassing the compiler-generated services. For example, hidden vptrs and pointers to virtual base classes can make it difficult to store C++ objects in databases or to move them across process boundaries, so you may wish to emulate these features in a way that makes it easier to accomplish these other tasks. From the point of view of efficiency, however, you are unlikely to do better than the compiler-generated implementations by coding these features yourself.

Back to Item 24: Understand the costs of virtual functions, multiple inheritance, virtual base classes, and RTTI   
  Continue to Techniques
6 In July 1995, the °ISO/ANSI committee standardizing C++ added a requirement that STL iterators support the "->" operator, so it->second should now work. Some STL implementations fail to satisfy this requirement, however, so (*it).second is still the more portable construct.
Return
7 In July 1996, the °ISO/ANSI standardization committee declared that both named and unnamed objects may be optimized away via the return value optimization, so both versions of operator* above may now yield the same (optimized) object code.
Return
8 At least that's what's supposed to happen. Alas, some compilers treat T(lhs) as a cast to remove lhs's constness, then add rhs to lhs and return a reference to the modified lhs! Test your compilers before relying on the behavior described above.
Return