http://people.csail.mit.edu/jaffer/Geometry/Pyramids
	Packing Pyramids

The study of Caclulus often appeals to geometry for insight; and geometric insights are a basis for dimensionality checking. The integral of the identity function f(x)=x from 0 to L is L²/2, the area of right isosceles triangle having sides L. If the units of L are cm, then the units of the integral are cm².

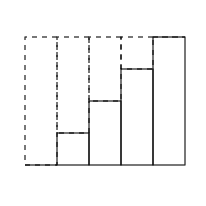The sum of the identity function at integer values from 0 to L is L·(L+1)/2. How can this be interpreted geometrically? By rotating a copy 180°, we get L+1 pairs whose lengths sum to L. This area is also (L²+L)/2. By removing one of the pairs, the area would be reduced to L²/2.

Aligning the two copies into a square results in a 1-unit gap in each of the L columns. This interpretation will be important later.

How are the units of the L term reconciled with L²? The +1 in (L+1) originates in the step between successive values. If the step is instead +2, then the sum is L·(L+2)/4. So the +2 has the same unit as L.

The extra factor of 2 in the denominator is also proportional to the step. Because we were summing just the identity function values, there are fewer of them when the step is increased. Proper analogy to the integral would compute the sum of the product of the identity function and the step (dx).

How does this generalize to higher dimensions? To the right is a construction visualizing the sum of a rising factorial, (x)⁽²⁾=x·(x+1).

Having no symmetry, this at first seems like an uninteresting object; but notice that the sum of (x)⁽²⁾ between 0 and L is L·(L+1)·(L+2)/3. If we change variable K=1+L, then the sum is K·(K+1)·(K-1)/3. This is equal to (K³-K)/3; which suggests that three of these objects could be combined with K unit cubes into a large cube. But which K cubes? Martin Jaffer saw that the diagonal from the skinny ends of the pyramids to the region common to the three largest plates constituted the missing cubes.

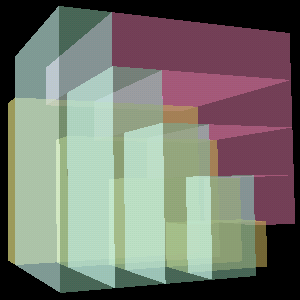The pyramids can indeed assemble to form a cube. To image at right shows three transparent asymmetrical 4x5x4 pyramids combined to form a 5x5x5 cube missing only the 5 cubes strung along its diagonal. Each pyramid has a volume of 40; the three of them together with the 5 cubes on the diagonal account for the cube volume of 125.

To the right is an exploded view of the cube linked to its VRML representation.

Although (L)⁽⁴⁾ must be divisible by 4, four dimensions does not seem to admit a simple decomposition of the hypercube:

e4 : (L-1)*L*(L+1)*(L+2);

             2      3    4
e4: - 2 L - L  + 2 L  + L

Inequalities

I wrote a program which, for rank r, side L, and a predicate function of r integers, counts how many of the cyclic permutations of the predicate function each of the L^r coordinates satisfy. From left to right, the numbers in brackets are the count of cubes belonging to no pyramids, the count of cubes belonging to one pyramid, the count of cubes belonging to two pyramids, and so on.

rank 2: y > z

rank 2 pyramids (side= 4) of size 6: [4 12 0]

For integer coordinates (x, y), the two triangles are those squares whose centers satisfy:

• y > z
• z > y

These two triangles are obviously exclusive. Squares on the diagonal, y=z, are not in either triangle.

rank 3: x > z and y >= z

rank 3 pyramids (side= 4) of size 20: [4 60 0 0]

For integer coordinates (x, y, z), the three pyramids are those cubes whose centers satisfy:

• x > y and x >= z
• y > z and y >= x
• z > x and z >= y

One axis is distinguished by being the stacking direction. The other two grow as one moves in the stacking direction. If both predicates were `>', then locations where the largest coordinate was repeated would be orphaned.

rank 4: w > z and x >= z and y >= z-1

rank 4 pyramids (side= 4) of size 78: [4 192 60 0 0]

rank 4: w > z+1 and x > z and y >= z

rank 4 pyramids (side= 4) of size 30: [136 120 0 0 0]

rank 4: w > z and x > z and y >= z

rank 4 pyramids (side= 4) of size 50: [56 200 0 0 0]

rank 4: w > z and x >= z and y >= z

rank 4 pyramids (side= 4) of size 70: [4 224 28 0 0]

rank 5: > > >= >=

(rank 5: v > z and w > z and x >= z and y >= z)

rank 5 pyramids (side= 4) of size 184: [104 920 0 0 0 0]

rank 6: > > >= >= >=

rank 6 pyramids (side= 4) of size 692: [238 3564 294 0 0 0 0]

rank 7: > > > >= >= >=

rank 7 pyramids (side= 4) of size 1952: [2720 13664 0 0 0 0 0 0]

rank 8: > > > >= >= >= >=

rank 8 pyramids (side= 4) of size 7576: [8104 54256 3176 0 0 0 0 0 0]

a > b and a >= c and a >= d and not (a = c and b = d)

rank 4 pyramids (side= 3) of size 19: [9 68 4 0 0]

rank 4 pyramids (side= 4) of size 64: [16 224 16 0 0]

rank 4 pyramids (side= 5) of size 160 [25 560 40 0 0]

rank 4 pyramids (side= 6) of size 335: [36 1180 80 0 0]

a > b and a >= c and a >= d and not (a = c and b >= d)

rank 4 pyramids (side= 3) of size 18: [9 72 0 0 0]

rank 4 pyramids (side= 4) of size 60: [16 240 0 0 0]

rank 4 pyramids (side= 5) of size 150: [25 600 0 0 0]

rank 4 pyramids (side= 6) of size 315: [36 1260 0 0 0]

(0 0 0 0)
(0 1 0 1)
(0 2 0 2)
(1 0 1 0)
(1 1 1 1)
(1 2 1 2)
(2 0 2 0)
(2 1 2 1)
(2 2 2 2)

The number of missed cubes is L². So the volume of each of the pyramids is:

L4 - L2 4

=

(L - 1) · L · L · (L + 1)  4

,

which is somewhat like a factorial product.

How do we construct the predicate for Rank 5? a > b allows only one of the pyramids to claim the cube when adjacent coordinates are the greatest. We need to select one pyramid when a = c are the greatest (a = d is the same as a = c when the coordinates are rotated). The only other rotation of (2,1,2,1,1,1) satisfying a > b is (2,1,1,1,2,1). The clause suppressing one of these must involve d.

Rank 5 pyramids fill the whole cube except for the diagonal:

a > b and a >= c and a >= d and a >= e and not (a = c and a > d)

rank 5 pyramids (side= 3) of size 48: [3 240 0 0 0 0]

rank 5 pyramids (side= 4) of size 204: [4 1020 0 0 0 0]

rank 5 pyramids (side= 5) of size 624: [5 3120 0 0 0 0]

e5 : factor((L^5-L)/5);

                             2
    (-1 + L) L (1 + L) (1 + L )
e5: ---------------------------
                 5

I wasn't expecting number theory to figure in pyramid packing; but prime ranks clearly pack better than composite ranks.

Once More, With Rigor

These predicates are related by cyclic permutation of their arguments:

r = 2

P_2,1(a,b) = a > b
P_2,2(a,b) = b > a

The area of a stepped triangle with side L will be the area of the smallest square enclosing both triangles minus the L (unit squares) of the diagonal; divided by the number of triangles: (L²-L)/2

Diagonal coordinate tuples are of the form (m,m,...,m), and are never part of a pyramid; all predicates P will be false for diagonal arguments. So a predicate P will be true only when at least one coordinate is less than m. Because each cyclic permutation of the arguments is associated with a pyramid, we can constrain P_r,1(a,b,...) so that a > b without loss of generality.

r = 3

a b c
m * m
m * *

Because a > b, P_3,1 of (non-indentity) cyclic permutations of these rows returns false. Because P_3,1 is true whether or not c is m, the first coordinate of P_3,1 is greater or equal to the third coordinate:

P_3,1(a,b,c) = a > b and a >= c
P_3,2(a,b,c) = b > c and b >= a
P_3,3(a,b,c) = c > a and c >= b

The volume of a pyramid with side L is the area of the smallest cube enclosing all the pyramids minus the L (unit cubes) of the diagonal; divided by the number of pyramids: (L³-L) / 3

r = 4

a b c d
m * m m	+
m * m *	P2,1(b,d)
m * * m	+
m * * *	+

The "m * m *" row will be matched by both P_4,1 and P_4,3. There are L²-L=L·(L-1) cases where both a = c and b = d, but a ¬= b. This product is not necessarily divisible by 4; so there is no way to allocate those unit cubes evenly 4 ways for every L. Thus the 4-dimensional case will have more than just the diagonal unit hypercubes vacant.

The predicate must return false for half of the cases where a = c and b ¬= d. This is the behavior of P_2,1(b,d).

P_4,1(m,b,m,d) = P_2,1(b,d) = b > d

The complete predicate is:

P_4,1(a,b,c,d) = a > b and a >= c and a >= d and (a > c or a = d or b > d)

The volume of a pyramid with side L is (L⁴-L²) / 4

r = 5

a b c d e	#
m * m m m	23	+
m * m m *	22	-
m * m * m	21	+
m * m * *	20	+
m * * m m	19	+
m * * m *	18	-
m * * * m	17	+
m * * * *	16	+

Cases 16, 17, 19, and 23 have only one contiguous group (with wraparound) of "m"s, so only one predicate will fire for them. Cases 18 and 20 are cyclic permutations, as are 21 and 22. Cases 20 and 21 differ in a single coordinate; so we choose them to inhibit the predicate:

P_5,1(a,b,c,d,e) = a > b and a >= c and a >= d and a >= e and (a > c or a = d)

Because r is prime, no cyclic permutation (other than identity) aliases itself; thus the only missing coordinate tuples are on the diagonal. The volume of a pyramid with side L is (L⁵-L) / 5

r = 6

a b c d e f	#
m * m m m m	47	+
m * m m m *	46	+
m * m m * m	45	P2,1(b,e)
m * m m * *	44	+
m * m * m m	43	-
m * m * m *	42	P3,1(b,d,f)
m * m * * m	41	+
m * m * * *	40	+
m * * m m m	39	+
m * * m m *	38	-
m * * m * m	37	-
m * * m * *	36	P4,1(b,c,e,f) | P4,1(c,e,f,b)
m * * * m m	35	+
m * * * m *	34	-
m * * * * m	33	+
m * * * * *	32	+

Cases 32, 33, 35, 39, and 47 have only one contiguous group of "m"s, so only one predicate will fire for them.

Case 42 is claimed by P_5,1, P_5,3, and P_5,5; so it resolves the remaining arguments by calling P_3,1(b,d,f). Cases 36 and 45 are claimed by P_5,1 and P_5,4. Case 45 is resolved by calling P_2,1(b,e). Case 36 is trickier. Of the four variables, b, c, e, and f, we can assume that the highest value occurs in either b or c. So Case 36 is resolved by the logical disjunction (or) of P_4,1(b,c,e,f) and P_4,1(c,e,f,b) [=P_4,2(b,c,e,f)].

Cases 46 and 43 are cyclic permutations, as are cases 44 and 37, cases 41 and 38, and cases 40 and 34. In the table above, cases 43, 37, 38, and 34 are suppressed; the rest are allowed.

As the predicates become larger, expression using only inequalities becomes difficult to read. Here is the predicate written in Scheme:

(define (P6 a b c d e f)
  (and (> a b) (>= a c) (>= a d) (>= a e) (>= a f)
       (case (booleans->integer #t #f (= a c) (= a d) (= a e) (= a f))
	 ((43 37 38 34) #f)
	 ((36) (or (P4 b c e f) (P4 c e f b)))
	 ((42) (P3 b d f))
	 ((45) (P2 b e))
	 (else #t)
	 )))

#t is true; #f is false. =, >, and >= are numerical predicates. The function booleans->integer returns a binary integer whose digits are 1 for #t and 0 for #f.

rank 6 pyramids (side= 7) of size 19544 
#(385 117264 0 0 0 0 0) 
rank 6 pyramids (side= 6) of size 7735 
#(246 46410 0 0 0 0 0) 
rank 6 pyramids (side= 5) of size 2580 
#(145 15480 0 0 0 0 0) 
rank 6 pyramids (side= 4) of size 670 
#(76 4020 0 0 0 0 0) 
rank 6 pyramids (side= 3) of size 116 
#(33 696 0 0 0 0 0) 
rank 6 pyramids (side= 2) of size 9 
#(10 54 0 0 0 0 0) 
rank 6 pyramids (side= 1) of size 0 
#(1 0 0 0 0 0 0) 

Derived in a later section, the volume of a pyramid with side L is (L⁶-L³-L²+L) / 6

e1 : factor((L^6-L^3-L^2+L)/6);

                                  3
    (-1 + L) L (1 + L) (-1 + L + L )
e1: --------------------------------
                  2 3

r = 7

a b c d e f g	#			a b c d e f g	#
m * m m m m m	95	+		m * * m m m m	79	+
m * m m m m *	94	+		m * * m m m *	78	+
m * m m m * m	93	-		m * * m m * m	77	+
m * m m m * *	92	-		m * * m m * *	76	+
m * m m * m m	91	+		m * * m * m m	75	+
m * m m * m *	90	+		m * * m * m *	74	+
m * m m * * m	89	-		m * * m * * m	73	-
m * m m * * *	88	-		m * * m * * *	72	-
m * m * m m m	87	-		m * * * m m m	71	+
m * m * m m *	86	-		m * * * m m *	70	+
m * m * m * m	85	-		m * * * m * m	69	+
m * m * m * *	84	-		m * * * m * *	68	+
m * m * * m m	83	-		m * * * * m m	67	+
m * m * * m *	82	-		m * * * * m *	66	+
m * m * * * m	81	-		m * * * * * m	65	+
m * m * * * *	80	-		m * * * * * *	64	+

This treatment is similar to case r = 5. One (of many possible) predicate is:

(define (P7 a b c d e f g)
  (and (> a b) (>= a c) (>= a d) (>= a e) (>= a f) (>= a g)
       (case (booleans->integer #t #f (= a c) (= a d) (= a e) (= a f) (= a g))
	 ((72 73 80 81 82 83 84 85 86 87 88 89 92 93) #f)
	 (else #t)
	 )))

rank 7 pyramids (side= 6) of size 39990 
#(6 279930 0 0 0 0 0 0) 

Because r is prime, no cyclic permutation (other than identity) aliases itself; thus the only missing coordinate tuples are on the diagonal. The volume of a pyramid with side L is (L⁷-L) / 7

Binomial Recurrences

(1 + a)r =

(

r 0

)

a0+

(

r 1

)

a1+ . . . +

(

r r

)

ar

In this unit growth on half of the hyperfaces of the hypercube, the constant 1 term corresponds to intersection of those new plates. The non-intersecting added volumes are counted by the terms of the binomial expansion except the first and last. If those non-intersecting volumes can be separated into r groups, then these 1-thick volumes can be stacked into r pyramids.

The diagonal through the center of both squares has a two-fold axis of symmetry.

The diagonal through the center of both cubes has a three-fold axis of symmetry. In both cases, the binomial terms greater than one are multiples of r. Thus each unit subcube has a place to go when the figure is rotated around this diagonal axis.

As established before, more than just the diagonal unit cubes are missing when rank 4 pyramids are combined. Taking the finite difference of the formula for volume derived previously gives the incremental volume of the construction.

e4 : f(L):=L^4-L^2;

f(L): f(L)

e4 : f(a+1) - f(a);

             2      3
e4: 2 a + 6 a  + 4 a

e5 : f(L): L^5 - L;

f(L): f(L)

e5 : f(a+1) - f(a);

              2       3      4
e5: 5 a + 10 a  + 10 a  + 5 a

It seems that prime values of r lead to r-fold rotational symmetry. Composite values of r have much less, if any, symmetry.

Moebius Inversion

Let R denote the cyclic permutation of the coordinates in Rⁿ and, for each integer i let Rⁱ denote the i-th power of R. For each divisor d of n, the number f(d) of lattice points in the cube that are fixed by R^d is L^(n/d). This includes all the points fixed by R^e for every divisor e of d. We want to be able to compute the number g(d) of points fixed by R^d which are NOT fixed by any R^e with e < d dividing d. In the special case d = n, where Rⁿ is the identity mapping, that will be the number of points in the cube which are not in the exceptional set, and the number in a single fundamental domain will then be g(n)/n.

We have the relation f(d) = sum {g(e) | e divides d}. We can then apply the Moebius inversion formula to compute g(d) in terms of f, namely, g(d) = sum{µ(e) · f(d/e) | e divides d}, where µ is the Moebius function, defined as follows: µ(d) is 0 if d is not square-free; if d is square free, µ(d) is 1 or -1 according to whether d is the product of an even or an odd number of primes. For example, 1 is a product of no primes and µ(1) = 1, while µ(p) is -1 for any prime p. [The Moebius inversion formula is really just a kind of inclusion-exlusion principle.]

So, you just have to apply that the function f(d) = L^(n/d) and compute g(n), i.e.
g(n) = sum{µ(d) · f(n/d) | d divides n} = sum{µ(d) · L^d | d divides n}.
As noted above, µ(d) is 0 unless d is square free. Therefore, if p, q, r, ... are the distinct primes dividing n, you have

g(n) =	Ln - sum{L(n/p) | p divides n; p prime}
	+ sum{L(n/(p q)) | p, q divide n; p, q prime; p < q}
	- sum{L(n/(p q r)) | p, q, r divide n; p, q, r prime; p < q < r}
	+ etc.

In particular, if n is prime, we get g(n) = Lⁿ - L and the number of points in the fundamental domain is g(n)/n. If n is the square of a prime p, g(n) = Lⁿ - L^p and we divide that by n. If n is the product of two distinct primes p, q, we get g(n) = Lⁿ - L^p - L^q + L. Thus, letting h(n) denote the number of points in the fundamental domain, we have:

h(2) = (L2 - L) / 2

h(3) = (L3 - L) / 3

h(4) = (L4 - L2) / 4

h(5) = (L5 - L) / 5

h(6) = (L6 - L3 - L2 + L) / 6

h(7) = (L7 - L) / 7

h(8) = (L8 - L4) / 8

rank 2 pyramids (side= 4) #(4 6) 

rank 3 pyramids (side= 4) #(4 0 20) 

rank 4 pyramids (side= 5) #(5 10 0 150) 

rank 5 pyramids (side= 5) #(5 0 0 0 624) 

rank 6 pyramids (side= 6) #(6 15 70 0 0 7735) 
rank 6 pyramids (side= 5) #(5 10 40 0 0 2580) 
rank 6 pyramids (side= 4) #(4 6 20 0 0 670) 
rank 6 pyramids (side= 3) #(3 3 8 0 0 116) 
rank 6 pyramids (side= 2) #(2 1 2 0 0 9) 
rank 6 pyramids (side= 1) #(1 0 0 0 0 0) 

rank 7 pyramids (side= 6) #(6 0 0 0 0 0 39990) 

rank 8 pyramids (side= 6) #(6 15 0 315 0 0 0 209790) 

Number Theory

For prime r and integer L, r divides L^r - L.

For positive L, this follows from being able to split L^r cubes r ways, excepting the L cubes on the diagonal.

For L=0, it is trivially true.

For negative L and odd prime r: (-L)^r - (-L) = -(L^r - L).

For negative L and r=2: (-L)² - (-L) = L² + L. If L is odd, then L² + L will be even (hence divisible by r=2); If L is even, then L² + L will be even.

This formula looks very familiar... Its a restatement of Fermat's little theorem! Saying that r divides L^r - L is equivalent to saying L^r is congruent to L mod r.

For integer L, 4 divides L⁴ - L².

This is easy to see by factoring L⁴ - L²: L⁴ - L² = (L - 1) · L · L · (L + 1) If L is even, then the two factors of L are divisible by 4. If L is odd, then both L-1 and L+1 will be even; again divisible by 4.

The general case leads to an extension of Fermat's Little Theorem:

sum{µ(d) · L^d | d divides n} = 0 mod n

Although not well known, this result is not new:

C. J. Smyth,
A Coloring Proof of a Generalisation of Fermat's Little Theorem,
The American Mathematical Monthly, Vol. 93, No. 6 (Jun. - Jul., 1986), pp. 469-471

Conclusion

Identical pyramids (built of unit hypercubes) packing to occupy nearly all of integer-sided hypercubes is interesting in its own right. It involves an unusual type of geometric symmetry which is more stringent than just rotating a hypercube around one of its longest diagonals. In euclidean spaces with a composite (non-prime) number of dimensions, there are unit hypercubes (besides those centered on the diagonal) which can't be assigned to pyramids such that all the pyramids are identical.