The intree case

When identical agents engage in a pursuit with an intree assignment graph, since there is a stationary agent, it is relatively simple to guarantee that 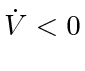$\dot{V} < 0$ by choosing an appropriate $\phi$ :

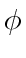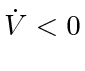Lemma 11   Unit speed pursuit of $n$ Dubins car agents with an intree assignment graph has the property $\dot{V} < 0$ and will rendezvous in finite time if the agents maintain their targets in the windshields of span 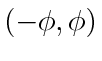$(-\phi, \phi)$ with $0 < \phi < \cos^{-1}\frac{n-2}{n-1}$ .

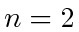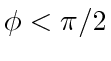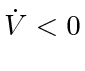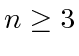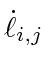PROOF. When $n = 2$ , one agent is stationary and one agent is moving; $\phi < \pi/2$ guarantees $\dot{V} < 0$ . When $n \ge 3$ , for an edge $e_{i, j}$ in an intree, we may express $\dot{\ell}_{i,j}$ similary as (8) (note the speeds are all $1$ ):

$$\dot{\ell}_{i,j} = -\cos \phi_i - \cos(\theta_j + \phi_j).$$ (23)

When the target agent 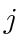$j$ is the root of the intree, the second term in (23) is zero since the root has no target and does not move. That is, $\dot{\ell}_{i,j} = -\cos \phi_i$ for at least one edge $e_{i, j}$ of the assignment graph. Let this edge be $e_{k,m}$ . Summing over all assignment edges yields

$$\dot{V} = -\cos \phi_k + \displaystyle\sum _{e_{i, j} \in E(G), e_{i, j} \ne e_{k,m}} -(\cos \phi_i + \cos(\theta_j + \phi_j)).$$ (24)

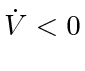$\dot{V} < 0$ is equal to

$$\cos \phi_k > \displaystyle\sum _{e_{i, j} \in E(G), e_{i, j} \ne e_{k,m}} - (\cos \phi_i + \cos (\theta_{j} + \phi_j)).$$ (25)

Assuming $0 < \phi < \pi/2$ , $\cos \phi_k > \cos \phi$ and $- \cos \phi + 1 > -(\cos \phi_i + \cos(\theta_j + \phi_j))$ , (25) is guaranteed by

$$\cos \phi > (n-2)(1 - \cos \phi),$$ (26)

which is equivalent to $0 < \phi < \cos^{-1}\frac{n-2}{n-1}$ . The finite time guarantee follows the argument from Corollary 9.