


Next: The intree case
Up: Guaranteed Rendezvous of Identical
Previous: A Candidate Lyapunov Function
Figure 4:
Two Dubins car agents in a cyclic pursuit.
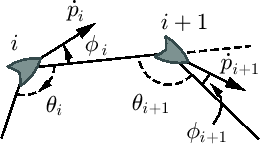 |
We start the analysis with cyclic pursuit: the  edges of
edges of  form a single polygon. Given the Dubins car model (1) and our control law (3), for two consecutive agents
form a single polygon. Given the Dubins car model (1) and our control law (3), for two consecutive agents  and
and  on the polygon, let
on the polygon, let  be either of the two angles of the polygon at vertex
be either of the two angles of the polygon at vertex  . For example, we may use the internal angles for simple (non-self-intersecting) polygons. In the special case of
. For example, we may use the internal angles for simple (non-self-intersecting) polygons. In the special case of 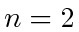 ,
,
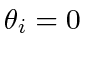 . Let
. Let 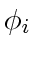 be the angle between
be the angle between 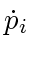 and the line segment from
and the line segment from 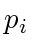 to
to 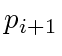 (see Fig. 4). Note that
(see Fig. 4). Note that 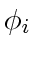 is not the same as
is not the same as 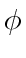 , half of the windshield span, which is fixed and the same for all
, half of the windshield span, which is fixed and the same for all  . The angle
. The angle 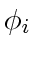 is positive if
is positive if 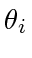 and
and 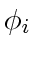 start from different sides with respect to the ray
start from different sides with respect to the ray
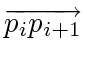 . The directions in which
. The directions in which
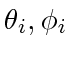 increase are marked with arrows in Fig. 4.
increase are marked with arrows in Fig. 4.
For a specific
 , agent
, agent  's movement will cause it to shorten at a rate of
's movement will cause it to shorten at a rate of
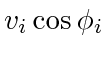 ; agent
; agent 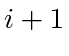 's movement will cause it to lengthen at a rate of
's movement will cause it to lengthen at a rate of
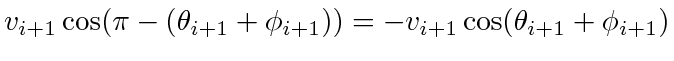 . The derivative of
. The derivative of
 is then
is then
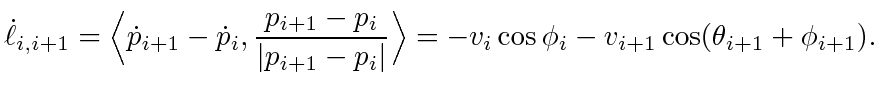 |
(8) |
After summing up (8) for all  and rearranging, we have for the cyclic case
and rearranging, we have for the cyclic case
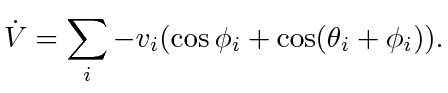 |
(9) |
For identical agents with unit speed 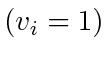 , (9) becomes
, (9) becomes
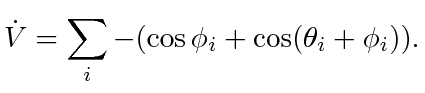 |
(10) |
We want to keep 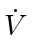 negative at all times prior to rendezvous. From (10) we get
negative at all times prior to rendezvous. From (10) we get
Lemma 3
For any integer 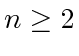 , the windshield angle
, the windshield angle
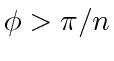 permits trajectories for which
permits trajectories for which
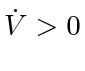 .
.
By Lemma 3, for any 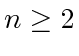 and
and
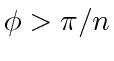 , pursuit cycles exist for which
, pursuit cycles exist for which
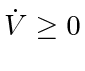 . We are now ready to give a sufficient condition for rendezvous.
. We are now ready to give a sufficient condition for rendezvous.
Theorem 4
Unit speed cyclic pursuit of  Dubins car agents will rendezvous if the agents maintain their targets in the windshields of span
Dubins car agents will rendezvous if the agents maintain their targets in the windshields of span
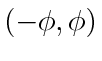 with:
with:
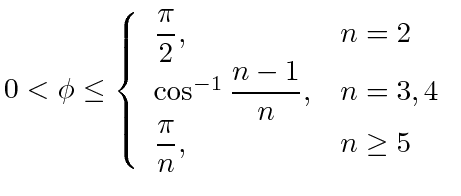 |
(11) |
The problem of how the agents can maintain their targets in a given windshield span, which is addressed with Proposition 16, is not part of this theorem. We proceed to prove Theorem 4 by first introducing several lemmas; essentially we want to show that if 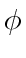 satisfies (11), then
satisfies (11), then
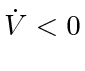 . We may then apply a Lyapunov theorem to conclude. To facilitate the discussion, define the first and second terms of
. We may then apply a Lyapunov theorem to conclude. To facilitate the discussion, define the first and second terms of 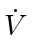 in (10) as
in (10) as
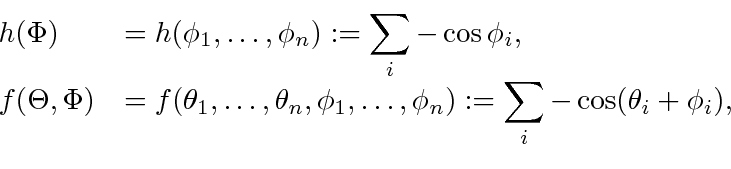 |
(12) |
and we have
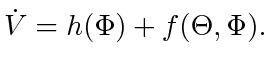 |
(13) |
For notational convenience, we use 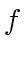 in place of
in place of
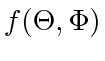 and
and  in place of
in place of 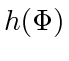 when it is appropriate to do so. By boundedness of the cosine function,
when it is appropriate to do so. By boundedness of the cosine function,
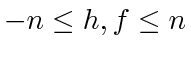 . Since
. Since
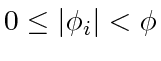 for all
for all  ,
,  can be made arbitrarily close to
can be made arbitrarily close to 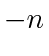 by lowering
by lowering 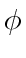 . Therefore, if for every fixed
. Therefore, if for every fixed  , there exists some
, there exists some
 such that
such that
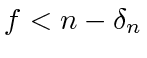 , some small
, some small 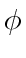 can be chosen to make
can be chosen to make
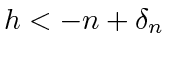 to obtain
to obtain
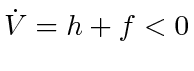 . The bound
. The bound
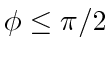 suffices for
suffices for 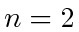 , which is straightforward to verify. Hence, we work with some
, which is straightforward to verify. Hence, we work with some 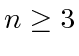 and first consider the case in which the pursuit cycle of the agents is a simple (non-self-intersecting) polygon; the self-intersecting polygon case then follows similarly. Recall that Lemma 3 suggests that we need
and first consider the case in which the pursuit cycle of the agents is a simple (non-self-intersecting) polygon; the self-intersecting polygon case then follows similarly. Recall that Lemma 3 suggests that we need 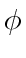 to be no more than
to be no more than  . As we assume that
. As we assume that
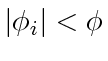 for all
for all  , we need
, we need
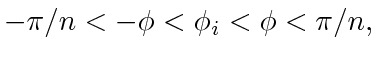 |
(14) |
adding
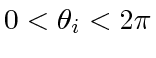 gives,
gives,
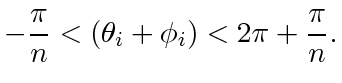 |
(15) |
We partition the 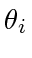 's satisfying (15) into two disjoint sets
's satisfying (15) into two disjoint sets
![\begin{displaymath}\begin{array}{ll} \Theta_{out} &= \{(\theta_1, \ldots,\theta_...
...a_i + \phi_i \in [\frac{\pi}{2}, \frac{3\pi}{2}]\}. \end{array}\end{displaymath}](img129.gif) |
(16) |
On
 , for at least one
, for at least one  ,
,
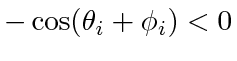 . We immediately have
. We immediately have 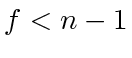 on
on
 . The following lemma tells us how
. The following lemma tells us how 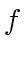 behaves on
behaves on
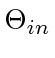 .
.
Lemma 5
Unit speed cyclic pursuit of  Dubins car agents with simple polygon pursuit cycle and satisfying (14) has the property that
Dubins car agents with simple polygon pursuit cycle and satisfying (14) has the property that
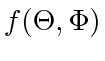 has a single stationary point on the interior of
has a single stationary point on the interior of
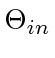 .
.
PROOF. If we fix 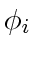 's, then
's, then 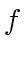 , as a linear combination of cosine functions of
, as a linear combination of cosine functions of 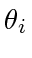 's, is bounded and continuous. Recall that for simple polygons, we may use the internal angles as
's, is bounded and continuous. Recall that for simple polygons, we may use the internal angles as 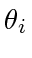 's. A simple polygon has the property that its internal angles sum up to
's. A simple polygon has the property that its internal angles sum up to 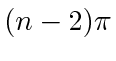 [35], which gives us,
[35], which gives us,
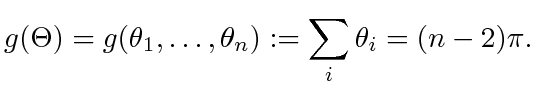 |
(17) |
Again, we use 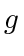 in place of
in place of 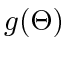 for notational convenience. Both
for notational convenience. Both 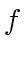 and
and 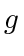 are analytic functions over the
are analytic functions over the 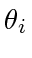 's. We may use
's. We may use
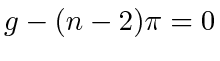 as the equality constraint to apply the method of Lagrange multipliers [26] over
as the equality constraint to apply the method of Lagrange multipliers [26] over 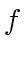 . The method produces the Lagrangian,
. The method produces the Lagrangian,
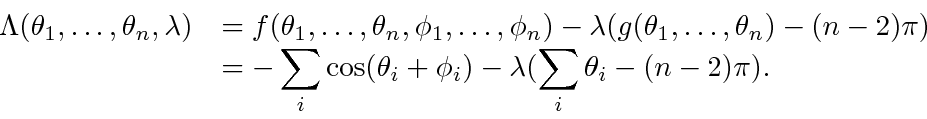 |
(18) |
The possible stationary points of 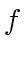 satisfy
satisfy
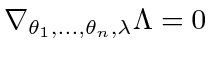 , or equivalently,
, or equivalently,
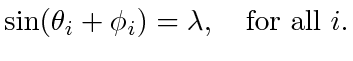 |
(19) |
From (14) and (17),
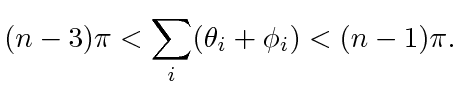 |
(20) |
As a side note, the
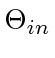 slice may be empty when
slice may be empty when 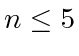 by the first inequality of (20). For any
by the first inequality of (20). For any 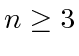 , by the pigeonhole principle [41], for at least one
, by the pigeonhole principle [41], for at least one  ,
,
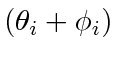 must be in the range
must be in the range
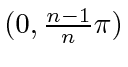 , which means that for that
, which means that for that  ,
,
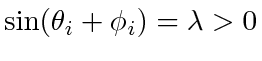 . By (19), for all
. By (19), for all  ,
,
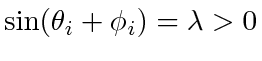 . This forces
. This forces 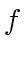 to have a single stationary point on the interior of
to have a single stationary point on the interior of
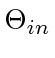 .
.
Lemma 6
At the stationary point in Lemma 5,
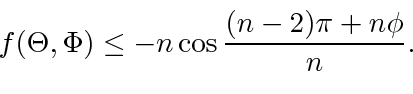 |
(21) |
The key property making the proof of Lemma 7 work is that the internal angles of any simple polygon in the plane sum up to
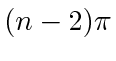 , which is less than
, which is less than 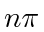 . We can then choose
. We can then choose 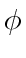 to make
to make
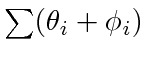 less than
less than 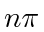 and the pigeonhole principle guarantees that some
and the pigeonhole principle guarantees that some
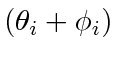 will be less than
will be less than 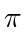 . In turn, it is guaranteed by the method of Lagrange multipliers that for all
. In turn, it is guaranteed by the method of Lagrange multipliers that for all  ,
,
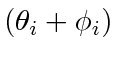 must take the same value
must take the same value 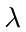 and must be less than
and must be less than 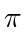 for
for 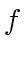 to take extreme values on the
to take extreme values on the
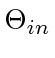 slice. Combining the
slice. Combining the
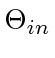 ,
,
 slices then gives the result. The same technique can be applied when the polygon is not a simple one:
slices then gives the result. The same technique can be applied when the polygon is not a simple one:
Lemma 8
Unit speed cyclic pursuit of  Dubins car agents with self-intersecting polygon pursuit cycle has the property
Dubins car agents with self-intersecting polygon pursuit cycle has the property
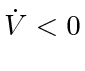 if the agents maintain their targets in the windshields of span
if the agents maintain their targets in the windshields of span
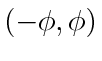 with
with 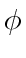 satisfying (11).
satisfying (11).
PROOF OF THEOREM 4. Having proved that the agents may choose a windshield span satisfying (11) to ensure
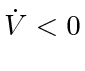 , by the standard Lyapunov theorem on asymptotic stability with respect to a set (see, e.g., [24]), all agents will rendezvous. The attractive set here is the ``diagonal'' in
, by the standard Lyapunov theorem on asymptotic stability with respect to a set (see, e.g., [24]), all agents will rendezvous. The attractive set here is the ``diagonal'' in
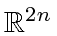 , in fact, its
, in fact, its 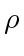 -neighborhood in which
-neighborhood in which 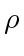 is the merging radius. Note that the introduction of
is the merging radius. Note that the introduction of 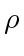 also addresses the issue that our
also addresses the issue that our 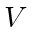 is not differentiable when some agents are in the same location; however, the result is valid even without this regularization (because a Lyapunov function with respect to an invariant set need not be differentiable on that set itself [24]).
is not differentiable when some agents are in the same location; however, the result is valid even without this regularization (because a Lyapunov function with respect to an invariant set need not be differentiable on that set itself [24]).
Once 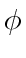 is fixed, the right side of (22) is determined, which leads easily to the existence of some
is fixed, the right side of (22) is determined, which leads easily to the existence of some
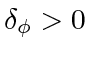 for which
for which
 for all time
for all time 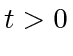 . This yields:
. This yields:
Corollary 9
System in Theorem 4 achieves rendezvous in finite time.
It is natural to ask whether the system is stable in the sense of Lyapunov: will some agents get arbitrarily far away from the rest during the converging process? The answer is no. Denoting  as the value of
as the value of 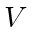 at
at  , we formalize the notion with the following proposition:
, we formalize the notion with the following proposition:
Proposition 10
For the system in Theorem 4,
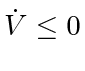 ensures that all agents are inside a bounding disc with radius at most
ensures that all agents are inside a bounding disc with radius at most
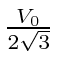 for all time
for all time  .
.
PROOF. In a cyclic pursuit, the candidate Lyapunov function, 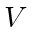 , is exactly the circumference of the pursuit cycle. Given any two different agents
, is exactly the circumference of the pursuit cycle. Given any two different agents  on the pursuit cycle, there are two disjoint, undirected paths from
on the pursuit cycle, there are two disjoint, undirected paths from  to
to 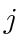 . One of these two paths must be no more than
. One of these two paths must be no more than 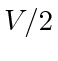 in total length and by repeated application of the triangle inequality, the straight line distance between
in total length and by repeated application of the triangle inequality, the straight line distance between  cannot exceed
cannot exceed 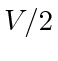 . The
. The  version of Jung's theorem [17,18] then tells us that there exists a bounding circle of the point set of all agents with radius no more than
version of Jung's theorem [17,18] then tells us that there exists a bounding circle of the point set of all agents with radius no more than
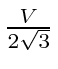 . Since
. Since
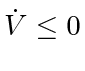 ,
, 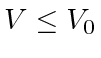 for all
for all  . Hence, there is no blowup prior to convergence (i.e., the system is stable in the sense of Lyapunov).
. Hence, there is no blowup prior to convergence (i.e., the system is stable in the sense of Lyapunov).



Next: The intree case
Up: Guaranteed Rendezvous of Identical
Previous: A Candidate Lyapunov Function
Jingjin Yu
2011-01-18
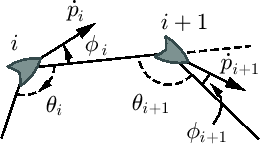
![]() , agent
, agent ![]() 's movement will cause it to shorten at a rate of
's movement will cause it to shorten at a rate of
![]() ; agent
; agent ![]() 's movement will cause it to lengthen at a rate of
's movement will cause it to lengthen at a rate of
![]() . The derivative of
. The derivative of
![]() is then
is then
![]() and
and
![]() , pursuit cycles exist for which
, pursuit cycles exist for which
![]() . We are now ready to give a sufficient condition for rendezvous.
. We are now ready to give a sufficient condition for rendezvous.
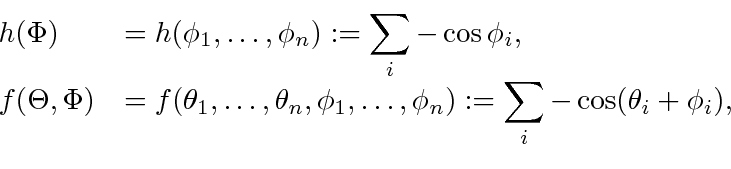
![\begin{displaymath}\begin{array}{ll} \Theta_{out} &= \{(\theta_1, \ldots,\theta_...
...a_i + \phi_i \in [\frac{\pi}{2}, \frac{3\pi}{2}]\}. \end{array}\end{displaymath}](img129.gif)
![]() , which is less than
, which is less than ![]() . We can then choose
. We can then choose ![]() to make
to make
![]() less than
less than ![]() and the pigeonhole principle guarantees that some
and the pigeonhole principle guarantees that some
![]() will be less than
will be less than ![]() . In turn, it is guaranteed by the method of Lagrange multipliers that for all
. In turn, it is guaranteed by the method of Lagrange multipliers that for all ![]() ,
,
![]() must take the same value
must take the same value ![]() and must be less than
and must be less than ![]() for
for ![]() to take extreme values on the
to take extreme values on the
![]() slice. Combining the
slice. Combining the
![]() ,
,
![]() slices then gives the result. The same technique can be applied when the polygon is not a simple one:
slices then gives the result. The same technique can be applied when the polygon is not a simple one:
![]() , by the standard Lyapunov theorem on asymptotic stability with respect to a set (see, e.g., [24]), all agents will rendezvous. The attractive set here is the ``diagonal'' in
, by the standard Lyapunov theorem on asymptotic stability with respect to a set (see, e.g., [24]), all agents will rendezvous. The attractive set here is the ``diagonal'' in
![]() , in fact, its
, in fact, its ![]() -neighborhood in which
-neighborhood in which ![]() is the merging radius. Note that the introduction of
is the merging radius. Note that the introduction of ![]() also addresses the issue that our
also addresses the issue that our ![]() is not differentiable when some agents are in the same location; however, the result is valid even without this regularization (because a Lyapunov function with respect to an invariant set need not be differentiable on that set itself [24]).
is not differentiable when some agents are in the same location; however, the result is valid even without this regularization (because a Lyapunov function with respect to an invariant set need not be differentiable on that set itself [24]).
![]() is fixed, the right side of (22) is determined, which leads easily to the existence of some
is fixed, the right side of (22) is determined, which leads easily to the existence of some
![]() for which
for which
![]() for all time
for all time ![]() . This yields:
. This yields:
![]() as the value of
as the value of ![]() at
at ![]() , we formalize the notion with the following proposition:
, we formalize the notion with the following proposition: