Abstract

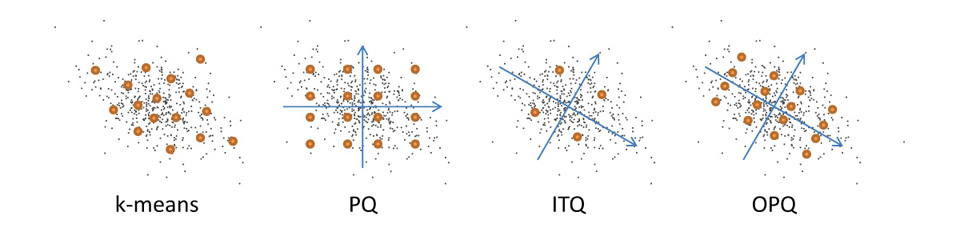
Product quantization (PQ) is an effective vector quantization method. A product quantizer can generate an exponentially large codebook at very low memory/time cost. The essence of PQ is to decompose the high-dimensional vector space into the Cartesian product of subspaces and then quantize these subspaces separately. The optimal space decomposition is important for the PQ performance, but still remains an unaddressed issue. In this paper, we optimize PQ by minimizing quantization distortions w.r.t. the space decomposition and the quantization codebooks. We present two novel solutions to this challenging optimization problem. The first solution iteratively solves two simpler sub-problems. The second solution is based on a Gaussian assumption and provides theoretical analysis of the optimality.

We evaluate our optimized product quantizers in three applications: (i) compact encoding for exhaustive ranking , (ii) building inverted multi-indexing for non-exhaustive search, and (iii) compacting image representations for image retrieval. In all applications our optimized product quantizers outperform existing solutions.