Namespace Balancing

Figure 11: There exists a strong correlation between a node's namespace and its utilization when the workload is uniform and capacities are constant.

Table I: Workload Skew under Namespace Balancing

Skew	Random		Balanced
	$r^{2}$	Succ. $\%$	$r^{2}$	Succ. $\%$
Uniform	$0.95$	$0.59$	$>0.99$	$1.00$
Zipf ($\alpha=0.8$)	$0.83$	$0.46$	$0.83$	$0.53$
Zipf ($\alpha=1.2$)	$0.61$	$0.27$	$0.57$	$0.29$
Zipf ($\alpha=2.4$)	$0.36$	$0.03$	$0.31$	$0.04$

These first experiments confirm that, under conditions of constant or near-constant capacity and uniform query distribution, simple namespace balancing is highly effective. However, when either of these conditions fails to hold, it is not.

In order to see the correlation between a node's namespace and its utilization, we ran a simple set of experiments in which we varied workload skew in a system that was performing no load balancing. We monitored the incoming routing and maintenance messages for each node and compared this to the fraction of the ID space for which that node was used as a hop or destination. We ran two sets of experiments: one where VS identifiers were chosen at random and a second where they were set offline to be exactly equal. This second case shows the best that namespace balancing could achieve. We used $4096$ nodes and set all node capacities so that they could route $100$ messages per second. No churn was used because the exactly equal ID computation is only performed offline. We varied workload skew from uniform to Zipf with $\alpha=2.4$. Because no active algorithm was used and there was no churn, each experiment stabilized immediately. Every node had one virtual server and there were $40960$ queries per second (10 queries per alive node).

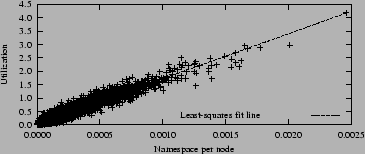
We plot the correlation between namespace and node utilization for a uniform workload in Figure 11. As is expected, the average namespace per node is $\frac{1}{4096} \approx .0002$. Because no load balancing is used, the distribution of namespaces is long-tailed. Analytically, the largest distance between two VSs should be $\frac{1}{4096} \times log (4096) \approx .0029$, close to the measured value of $.0025$. Utilizations with random IDs ranged from almost 0 to about 4. In contrast, the case where the namespaces were completely balanced yielded an extremely small range of utilizations from $0.55$ to $0.57$.

As we relax the assumption that workloads are uniform, the benefit in perfectly uniform address spaces declines. Table I shows how the correlation and success rates for queries decline as workload skew increases. Separate experiments confirm a similar decline as heterogeneity in nodes' capacities changes from a constant. We can conclude from this that, in order to achieve reasonable performance, a load balancing algorithm must include some workload parameter and cannot aim for address space balancing alone.