k-Choices Algorithm

k-Choices is a greedy, cost-based load balancing algorithm for structured overlays. It matches nodes' workload goals with guesses about how their choices of identifiers will affect both their own workloads and those of their neighbors. At each VS insertion, k-Choices minimizes the discrepancy between work and capacity by sampling from a small set of potential IDs. By limiting the number of potential IDs, k-Choices is practical for networks containing malicious participants.

k-Choices functions primarily at node join time as shown in k-Choices Node Join in Figure 3. When a node joins, it chooses a total target workload and an upper bound on the number of VSs to create (lines 1-2). Then, it invokes k-Choices VS Join and reduces its remaining capacity by the anticipated work of that VS (line 3). This continues until it has created $\kappa/2$ VSs or reached its target workload. Making several VSs together at join time amortizes the cost of sampling.

The join for each VS is composed of four steps, as shown in Figure 2 and in k-Choices VS Join in Figure 3. A small menu of potential IDs is chosen, limited by a well-known constant $\kappa$ (lines 1-2). These IDs are verifiable because they are all based on the certified $x$ and because $\kappa$ is bounded. To verify that a node is using a valid ID, $k$, another node simply has to check that there exists some $i < \kappa$ such that $k = h(x + i)$. Next, each potential ID's successor is probed to discover what is likely to happen were this VS to be placed at this location (line 4). It guesses that the current work for this location will be split based on the percentage of the address space the joining VS will take on (lines 6-7). The node uses this to compute the change from the current situation (line 8). Each term in the cost function is the difference between target work and real work. The first two terms are the sum of the differences if this VS is created and the last is the current situation. We normalize each term based on the node's capacity. Thus, the lower the cost, the smaller the difference between target and actual work. The last step of the join process is to join at the ID with lowest cost. Because nodes set their targets lower than their capacities, if all nodes minimized the mismatch $m = \vert t - w\vert = 0$, then loss would be zero.

If nodes do not attempt to perform any additional load balancing after joining, we say they are passive. Being passive has its advantages: no additional churn is induced through VS relocation. However, over time one of the other potential IDs for this VS can become significantly better in terms of improving target/workload mismatch.

If we permit reselection of IDs, we say that k-Choices is active. To minimize network probing, nodes reselect only a single VS ID at a time. They pick the $v \in$ VSset with the maximum mismatch. They check if any new ID for $v$ improves the aggregate mismatches of themselves and their neighbors by $\epsilon$, a parameter that dampens improvements of minimal benefit. If it does, the movement is performed. $\epsilon$ is application-dependent: when a system is used for routing, moving will be relatively painless, as VSs can gracefully notify incoming pointers of their departure; if objects are stored and need to be sent over the network, the cost might be significantly greater. Nodes only examine the possibility of relocating if they are overloaded or underloaded. If nodes have relocated more than VSset.size times and are still overloaded or underloaded, they create or destroy VSs within the range $(1, \kappa)$. In practice we found that nodes did not create more than a handful of additional VSs.

k-Choices possesses several attractive features and makes certain assumptions. When run in passive mode, it adds no reactive churn. In fact, without an active component, it requires natural churn. By making a good choice before routing is set up, objects are stored, or computations are started, k-Choices lessens or eliminates this reactive load balancing penalty. We assume that nodes do not lie or that Distributed Algorithmic Mechanism Design techniques could be used to encourage the truthfulness of the information they provide about load [19,41], another reason why verifiable IDs are important. We also assume that the system is not primarily being used for range queries. Limited ID assignment provably cannot balance load in this case [26].

Note that VSs could keep more accurate track of where work is landing in their namespace to make $w_{a}$ and $w_{s}^{(f)}$ more accurate. Instead, we decided to use a simple exponentially-weighted moving average to reduce the amount of state sent during probing.

Optimal ID Choice. k-Choices exhibits diminishing returns as $\kappa$ approaches the size of the namespace $D$. When $\kappa = D$, each joining VS would sample every possible ID (assuming a perfect hash function). In fact, it is feasible to find the ID (or IDs) with the lowest cost by examining only a few variables for each existing VS. While even this sampling would be prohibitively expensive in an implementation, performing it ``offline'' within a simulator is not.

For each potential successor $s$, we know its target $t_{s}$ and its actual work $w_{s}^{(n)}$. The goal is to find the percent of the address space $r$ between $pred(s)$ and $s$ that gives the minimum cost $c$ and to find what the cost is for this $s$. The optimal ID choice will be the $pred(s) + r \times dist(pred(s),s)$ with the globally lowest cost. We know that $w_{s}^{(n)} \geq 0$ and that $m_{s} = \vert t_{s} - w_{s}^{(n)}\vert$ is fixed regardless of the $r$ chosen. If we do not normalize for each node's capacity, there are four mutually exclusive cases for $r$ and $c$:

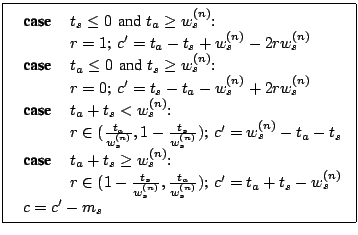
In cases 1 and 2, we do not eliminate $r$ because IDs cannot be identical. The actual choice will need to be a small distance away.