Serpentine Marbling

	http://people.csail.mit.edu/jaffer/Marbling/Serpentine
	Serpentine Marbling

In The Mathematics of Marbling, we explored simple linear and circular deformations and produced images which are clearly marbling, but do not look like the marbled forms artists create.

http://colloid.csj.jp/garelly/expo/con_index.html

Serpentine

This "Serpentine Marble" looks like a horizontal ten-tine comb was stroked upward while wiggling left and right in a sinusoidal path.

(Unfortunately, the high-resolution original from http://langmuir.chem.utsunomiya-u.ac.jp/colloid/photo/ is no longer available.)

Although the distance function to a sinusoid curve can be computed, it is easier to stroke tines vertically; and then add a horizontal displacement proportional to the sin(degrees) of each point's y-coordinate:
W_h(x, y) = (x - 20 · sin(2.5 · y), y)
The dark tone of the work is here produced by interposing a very dark double-wide band between each pair of the other paints.

[images are linked to PostScript files]

Marbling Backward

A nice feature of these particular straight and circular deformations is that the induced translations leave the parameter which controls that motion unaffected. In the linear case, the motion of a point is perpendicular to the controlling distance (point to line). In the circular case the rotational movement around the center does not affect the radius on which it depends.

For a given depth z, if we apply a deformation followed immediately by the same deformation but with negative z, the two motions are in opposite directions and leave the points where they started. ^(−z)F is thus the inverse transform of ^(z)F. The inverse-composite-map is simply the composite-map functions in reverse order with negated z:
F⁻¹ = F₁⁻¹ ∘ F₂⁻¹ ∘ … ∘ F_n⁻¹
Where the previous algorithm took paint-circle coordinates and mapped them to their destinations, we can as easily take coordinates in the viewable area, transform them through the inverse-composite-map, and identify which paint band they come from. Since my paint bands are concentric circles, there is no need to explicitly enumerate them. I just calculate the distance from the virtual paint center point, and assign a color (from a palette sequence of 12) with modular arithmetic.

This method eliminates restrictions on the number and thinness of paint bands. Only the viewable area is rendered; one no longer needs to experiment with circle increments and the mostly unseen outer paint-circles.

But unlike the contoured images anti-aliased by GhostScript, assigning the color to a pixel based just on the mapped coordinates' truncated distance from the origin results in aliasing artifacts where multiple bands squeeze through one pixel cell. Computing colors for sub-sampled points would be slow; but the color-number's fractional part can be used to interpolate between the colors of the two bands whose border is closest.

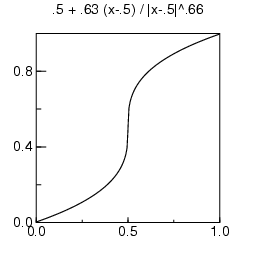
The resulting image is perhaps too soft. Using an S-shaped function to sharpen the distinction between the bands reaches a happy medium.

To the left is the circular marble rendered as nested contours. To the right is the circular marble raster-rendered with the S-shaped function.

The next chapter attempts more complicated effects acheived by physical paint marbling.

I am a guest and not a member of the MIT Computer Science and Artificial Intelligence Laboratory. My actions and comments do not reflect in any way on MIT.
		Topological Computer Graphics
	agj @ alum.mit.edu	Go Figure!