http://people.csail.mit.edu/jaffer/cool/Aperture
	Optics for Passive Radiative Cooling Aubrey Jaffer

The Second Law of thermodynamics dictates that no net radiative energy transfers between two objects at the same temperature.

Thus the blackbody radiative flux through an aperture can be no greater than that produced by a blackbody at the same temperature having that aperture as its surface.

Therefore, blackbody radiation cannot be concentrated by any arrangement of mirrors. The rate of cooling is limited by the smallest aperture through which the blackbody radiation all flows.

But this does not mean that optics are useless. The blackbody radiation is proportional to the radiating surface area integrated with the angle over which it radiates. While mirrors cannot increase the effective radiating area, they can channel the radiation emitted over a 180° cone (hemisphere) into a narrower cone.

This turns out to be more than just interesting; it makes radiative cooling practical in locations where the view to the horizon is obstructed.

Passive optical systems are reciprocal; if light can travel from point-A to point-B, then light can travel from point-B to point-A. For radiative cooling applications this means it is desirable for the blackbody radiator to see only those regions of sky far above the horizon. Atmosphere near the horizon is warmer than atmosphere near the zenith. If in view of the radiator, warm atmosphere will transfer heat into the radiator, opposing the desired cooling.

Thermal-infrared optical systems are further constrained in that the only way to obstruct the view between points A and B is by reflection or refraction. A material which absorbs thermal-infrared radiation also emits it.

What then, is the optimal aperture for radiative cooling? Through analysis of the properties of the atmosphere we can determine a threshold angle t (from the horizontal), such that rays entering from angles above t should be directed to the radiating element; while rays entering at angles below t should be reflected away.

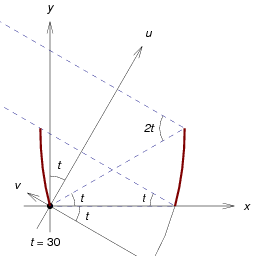Consider the parabolic section on the right side of the diagram. It directs all rays from angle t onto the focus point at the origin. As the angle of incidence increases, so does the angle of reflection, illuminating the radiator at the base (and some of the rays will strike the radiator directly). As the angle of incidence decreases, so does the angle of reflection, directing the rays to the parabola on the other side, which directs them up upward.

The top of each parabolic section is perpendicular to the base (on the x axis). The u and v axes are the coordinate system of the right-side parabola. This reflector configuration is a compound parabolic concentrator[48] (CPC). The diagram is linked to a PDF of these diagrams with t ranging from 10° to 50°. An animation of these diagrams is also available.

The diameter at the top of the CPC is b/cos(t), where b is the diameter of the base. If this configuration is optimal (vis-a-vis the Second Law), then the flux through the (larger) top aperture for angles greater than t should equal the hemispheric flux from the base. Lets examine the case of a surface of rotation around the midpoint of the base of diameter b=1. From an inclination θ, the aperture flux around the circle is 2π·sin(θ)/cos(t)·dθ. Integrating from θ=t to θ=π/2 yields a total aperture flux of 2π, independent of t. t=0 is the hemispheric case; so the assertion is verified.

It is remarkable that the Second Law of Thermodynamics places hard limits on geometrical optics. This equivalence above was easily found; no attention was paid to the nonuniform distribution of rays striking the target at any particular angle of incidence.

Ray-tracing a surface of revolution of this system shows the abrupt transition between the radiator being hidden and being exposed. This image is viewing the aperture from 28° above the horizon from a distance 200 times the diameter of the aperture (as through a telephoto lens). The dark bands at the left and right extremes of the interior are artifacts of the POV-Ray simulation.
This image is viewing the aperture from 30° above the horizon, which is the threshold angle. The aperture rests on a red and white checkerboard, whose distorted reflection is visible in the aperture.

This image is linked to a PDF of images with the viewing angle ranging from 0° to 90°. An animation of these images is also available.
This image is viewing the aperture from 32° above the horizon. The aperture interior is almost completely filled with the distorted image of the checkerboard. A small portion of the undistorted checkerboard is visible just above the nearest edge of the aperture.

The top of the aperture being larger than the radiating base means that the directivity comes at the price of area. The aperture efficiency of this CPC is cos²(t), which for t=30° is 75%.

Solar Irradiance

Direct solar irradiance from below the threshold angle will not impinge on the base of the CPC. But for solar irradiance from above the threshold angle, all that enters the upper aperture will reach the base. That is A·sin(θ)/cos²(t), which for overhead sun is greater than that which would fall on the base without the aperture.

Stackable Apertures

Using the same parabolic section, but forming it into a square box (here inscribed in the previous cylinder) results in an aperture which can be arrayed together with no space wasted between them. This image is viewing the aperture from 28° above the horizon. There is more intrusion of the target into the aperture than with the cylindrical model. At 27° the aperture is nearly all sky.
This image is viewing the aperture from 30° above the horizon, which is the threshold angle.

This image is linked to a PDF of images with the viewing angle ranging from 0° to 90°. An animation of these images is also available.
This image is viewing the aperture from 32° above the horizon. The aperture interior is mostly filled with the distorted image of the checkerboard. At 33° and above the aperture is almost completely filled with the checkerboard.

Looking from a ray parallel to the sides, the transition zone is 4° (same as for the round aperture). Looking along the diagonal, the transition zone is only 2° (better than the round aperture).

So the square aperture has nearly optimal angular selectivity. The worst case (shown) transition zone is 6° wide, only 2° wider than for circular apertures.

An array of square aperture cells is not as tall as a single cell covering the same area and having the same threshold angle. The array of cells presents a lower wind load and can be adapted to sloping roofs (discussed later). To first approximation, the array of square cells uses the same amount of material as a single square cell.

An array of square apertures could be assembled as a lattice of (notched) extrusions.

Slope

For some sites, inclining the apertures could be beneficial. An aperture inclined toward the east would, in addition to cooling radiatively, collect and channel direct sunlight downward during the morning.

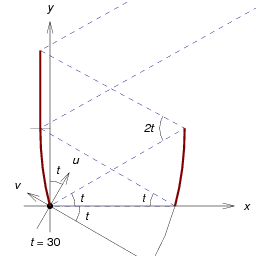Returning to the schematic, if the top edge of the left parabola is extended with a flat vertical mirror, it reflects some rays which would have exited toward the left to instead exit toward the right, but at the same inclination. So the cone of radiation for this configuration fits within the cone of radiation of the earlier CPC. And because every ray which exits the earlier CPC exits this one, it has the same cooling power as the earlier CPC.

This schematic is for a square CPC. As before, the indirect solar flux impinging on the base of the CPC will be equivalent to the indirect solar flux impinging on a totally exposed level disk having the same area as the base of the CPC.

The incidence of direct solar flux is more complicated. As before, no flux will impinge on the base while the solar inclination θ is less than t. With the sun at zenith, the base receives all the flux received through the top aperture, A/cos²(t).

With the sun on the left side, no flux will impinge on the base while θ is less than φ=atan(m·cos(t)/b), where m is the height of the mirror extension. Note that φ may be greater or less than t; in the diagram they are equal. The mirror casts a shadow on the plane of the upper aperture which is m/tan(θ) wide. When b/cos(t)>m/tan(θ), a strip of the aperture b/cos(t)-m/tan(θ) wide is illuminated.

With the sun on the right side, a strip of the aperture b/cos(t)-m/tan(θ) wide is illuminated twice. This is the same amount as was shaded with the sun at elevation θ on the left side.

Vertically extending one side of CPCs allows us to terrace rows of square CPCs to match the slope of any roof. Here is a design for a 3 by 5 terraced array of CPCs. This view is 10 times closer than the previous views; so it has noticeable parallax; the top row shows all sky while the lowest row shows mostly radiator.

The vertical mirror works to avoid obstacles even when it isn't extending with the parabolic section. Obstacles like chimneys can be shielded from radiating their heat into the CPC by interposing vertical aluminum flashing between the obstacles and the CPC.
If the slope of the roof is greater than the (tangent of the) threshold angle (which isn't the case shown), then the edge cells of the terraced radiator "sees" adjacent roof. This can be remedied by incorporating vertical reflective side panels.

Although not necessary, a reflective back panel has also been added at the top so that the (top) side edges of the assembly don't have a level miter at the highest cell.

Cover

For use in subtropical and temperate regions, there needs to be a way to temporarily disable roof panel radiation. Hinged reflective flaps along each row of cells can accomplish this. The top two images show a roof panel with flaps horizontal (covering the CPCs), pivoted on the black axles protruding from the right side. The bottom two images show a roof panel in the vertical (open) position. As was established earlier, vertical reflectors do not interfere with radiative cooling from the compound parabolic concentrators. The images on the right side paint the flaps with a checkerboard pattern in order to help distinguish the flaps from reflections.

High reflectivity surfaces are necessarily low emissivity; so when the roof panel is closed, it will not radiate much heat. To reduce convective heat losses, the assembly should be a sealed air space. So far the prototypes have had their checkerboard radiative targets in strips in contact with the lower CPC apertures. But they can be combined into a single continuous sheet along the bottom of the assembly.

A (inclined) flat-bottom, terraced roof panel without flaps is shown to the right. One with open flaps is shown below.

Conclusion