


Next: Implementation and Simulation Results
Up: Condition on Angular Velocity
Previous: Angular Velocity Condition
In the set of sufficient conditions stated in our earlier theorems that guarantees rendezvous, we have assumed that the assignment graph 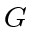 has a single connected component initially. We now show that the assumption of single connected assignment graph and agents stopping are not necessary by: 1. Allowing agents to perform reassignment. 2. Allowing agent without targets to merge with other agents within distance
has a single connected component initially. We now show that the assumption of single connected assignment graph and agents stopping are not necessary by: 1. Allowing agents to perform reassignment. 2. Allowing agent without targets to merge with other agents within distance 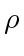 . Initially, the assignment graph
. Initially, the assignment graph 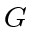 has
has  components: each component contains a single agent. Look at one such component
components: each component contains a single agent. Look at one such component 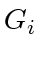 with a single agent
with a single agent  . If there are other agents within distance
. If there are other agents within distance 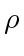 of
of  , they will merge with
, they will merge with  , therefore, we may assume that there are no other agents within distance
, therefore, we may assume that there are no other agents within distance 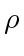 of agent
of agent  . To rendezvous with other agents, let agent
. To rendezvous with other agents, let agent  pick any target in its windshield and if it cannot find any, let it start turning. We will show that with two full turns, it can find agents at least
pick any target in its windshield and if it cannot find any, let it start turning. We will show that with two full turns, it can find agents at least 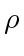 away from it or confirm that there are no such agents to conclude rendezvous is achieved. We call this procedure of finding new targets reassignment. We have the following:
away from it or confirm that there are no such agents to conclude rendezvous is achieved. We call this procedure of finding new targets reassignment. We have the following:
Proposition 17
By allowing merging and reassignment for agents that have no targets, bounded speed pursuit of  Dubins car agents will achieve rendezvous without the initial connectivity requirement, provided that the system will rendezvous if given a connected initial assignment graph and
Dubins car agents will achieve rendezvous without the initial connectivity requirement, provided that the system will rendezvous if given a connected initial assignment graph and
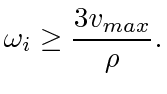 |
(41) |
Our sensing model (see Appendix A) may do without agents being distinguishable if agents are capable to take continuous videos of their targets in windshield. For agents moving at unit speed, such capability is not necessary provided that when an agent is confused by two possible targets that are colinear with it, it can follow the target that is closer. Such switching is a natural one since a closer target will block a more distant one, effectively removing the assumption requiring no visibility occlusion. Alternatively, if all agents simply send out a beacon signal, a closer agent will have a stronger signal than a more distant one. We have:
Proposition 18
By allowing merging and reassignment for agents that have no targets, as well as the ability for an agent to choose a closer agent as target when two possible targets become colinear with it, unit speed speed pursuit of  Dubins car agents will achieve rendezvous with
Dubins car agents will achieve rendezvous with
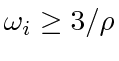 and windshield angle satisfying (27), without initial connectivity or agent distinguishability.
and windshield angle satisfying (27), without initial connectivity or agent distinguishability.
PROOF. Denoting agent  and its two possible targets
and its two possible targets 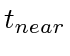 and
and 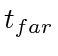 , when such switching of targets happens,
, when such switching of targets happens, 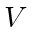 of the system cannot get larger since the affected term in
of the system cannot get larger since the affected term in 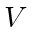 during a target switching will have
during a target switching will have
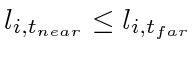 and
and
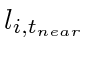 is always chosen. At the same time, Theorem 12 guarantees that
is always chosen. At the same time, Theorem 12 guarantees that 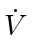 remains negative.
Proposition 18 also implies that agents will no longer need to stop before they all rendezvous.
remains negative.
Proposition 18 also implies that agents will no longer need to stop before they all rendezvous.



Next: Implementation and Simulation Results
Up: Condition on Angular Velocity
Previous: Angular Velocity Condition
Jingjin Yu
2011-01-18