Implementation and Simulation Results

A Java implementation was written to verify the theoretical developments, which focuses on the two key scenarios of rendezvous: assignment graph with a single cycle and assignment graph with a cycle plus branches. The program² was developed adhering to the Java 5 language standard under the Eclipse environment.

Discretization is necessary to implement the continuously evolving system. Sensing needs to be discretized because the Dubins car model allows jumps in angular velocity; therefore, there could be a large number of control switches within a short time interval. In our implementation, we divide the windshield into a left sector and a right sector. The triggering event is simulated by remembering the latest observation of the target agent $j$ 's relative position in pursuing agent $i$ 's windshield at time step $k$ ,

$$y_i[k] = \left\{ \begin{array}{ll} -1 & \textrm{agent $j$ is in ... ... of view} 1 & \textrm{agent $j$ is in the right sector}, \end{array} \right.$$ (42)

and comparing that with the next observation. If the agent is near the center of the windshield, we can give it $1$ or $-1$ . The quantized control can be encoded as

$$u_i[k] = \left\{ \begin{array}{ll} \omega & \textrm{$y_i[k] = 0, ... ... = 0, y_i[k - 1] = 1 $} u_i[k-1] & \textrm{otherwise}, \end{array} \right.$$ (43)

with $u_i[0] = 0$ by assumption. This control law can be expressed as an equivalent four state automaton. The implementation of an agent is therefore also quite simple, which enables the simulation to scale well with respect to the number of agents in the system. Plotting the Lyapunov function for systems with more than 10,000 agents can be handled quickly on our computer with a small memory footprint; smooth animation is possible for 100 agents, with the Lyapunov function and each $\ell _{i,i+1}$ plotted simultaneously in a separate window.

Figure 6: a) Eight-agent cyclic pursuit, which converges, with $\phi = 0.35$ and $\omega = 2.0$ b) Plot of the Lyapunov function for (a), with numbered lines being individual $\ell _{i,i+1}$ terms. c) Diverging case with $\phi$ changed to $0.6$ holding other conditions the same. The agents arrange themselves on a cycle quickly as they spin away from each other. Dots are the agents' positions as of the last snapshot. d) Plot of the Lyapunov function for (c). e) Eight-agent converging pursuit with agents $0, 4, 3$ and $5$ on a cycle; the branches are: $6 \to 2 \to 0$ , $7 \to 3$ , $1 \to 5$ . f) Plot of the Lyapunov function for (e).

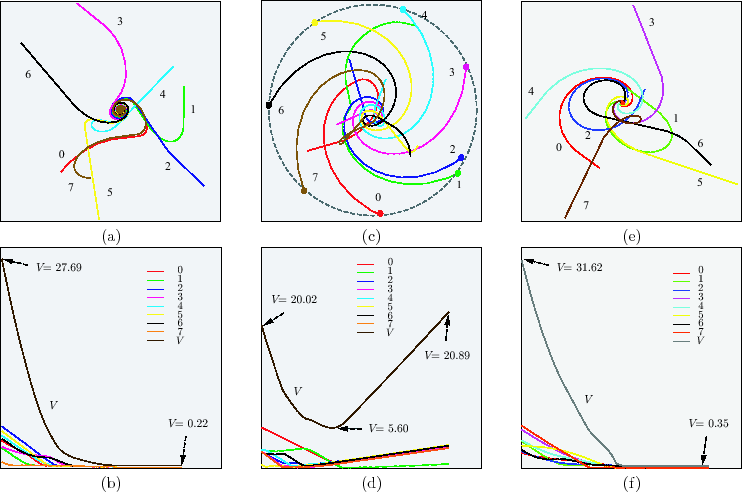To verify the cyclic pursuit theorems for the Dubins car model, each agent is assigned a unique integer identifier. For the single cycle case, we initialize the system by positioning the agents randomly and assigning each agent to the one with a preceding identifier; the first agent is assigned to the last one. The behavior of the cyclic pursuit is then observed by watching the agents' trajectories and a simultaneously drawn plot of the Lyapunov function, under different parameter settings. Since we want to observe the behavior of the cyclic pursuit with all agents, the merging radius $\rho$ is set to near zero to inhibit merging. For every attempted set of $n$ agents, the simulation indicates that $\phi = \pi/n$ is a tight rendezvous bound. As predicted, randomly positioned agents rendezvous when $\phi <\pi/n$ , but they will eventually diverge if $\phi$ is only $1\%$ above $\pi/n$ . In the latter case, the agents get closer quickly in the beginning as random arrangements appear to induce more negative $\dot{V}$ . Interestingly, the agents then tend to arrange themselves on a circle and eventually form a regular polygon, making $\dot{V}$ positive. We speculate that the continuous system has the same behavior, which is shown in [28,31] with different motion primitive and/or control law. Fig. 6 a) - d) shows both a converging and a diverging case with $n = 8$ . In the rendezvous case, $V$ does not go to zero because $\rho$ is set to be very small. The case with cycle plus branches is implemented similarly: we make a random cycle (with less than $n$ agents) and then attach the rest of the agents to the cycle in a random way. Its simulation behavior (a converging example is shown in Fig. 6 e) - f)) is very similar to the single cycle case.