



Next: Modellizzazione matematica
Up: Impostazione matematica del problema
Previous: Impostazione matematica del problema
Contents
Il metodo di ricostruzione che verrà esposto di seguito ci permetterà
di rimuovere la distorsione dovuta alle controparti negative e di ridurre il
noise. La ricostruzione potrà essere tuttavia affetta da
artefatti per la cui riduzione verranno proposte procedure adeguate.
Più avanti riprenderemo la descrizione della tecnica di chopping and
nodding già vista in §1.3 per poter descrivere l'algoritmo di inversione
usando una notazione consistente a quella di tutto il lavoro.
Come già detto nel capitolo precedente,
l'immagine astronomica risulta immersa in un fondo variabile, denominato
background, che chiameremo  nel seguito.
nel seguito.
Il segnale  che arriva dalla direzione di coordinate
che arriva dalla direzione di coordinate  , al tempo
, al tempo
 , nel punto
, nel punto  del piano immagine, è dato da:
del piano immagine, è dato da:
![\begin{displaymath}
s_{P}=T_{P}\times[f(x,y)+a(x,y,t)] \,\,
\end{displaymath}](img28.png) |
(2.1) |
dove  rappresenta la funzione di trasferimento del sistema,
rappresenta la funzione di trasferimento del sistema, 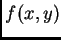 è il segnale proveniente dalla sorgente cosmica e
è il segnale proveniente dalla sorgente cosmica e  è il termine
di background.
è il termine
di background.
Il problema che ci si pone è quello di valutare la distribuzione 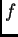 e
questo risulta possibile solo se si conosce effettivamente il background
e
questo risulta possibile solo se si conosce effettivamente il background
 .
.
Tramite osservazione con la tecnica di chopping, precedentemente
discussa, si era arrivati ad una possibile soluzione: facendo puntare
il telescopio verso una porzione di cielo senza segnale tramite spostamento
di  arcosecondi nella direzione
arcosecondi nella direzione 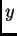 , si poteva ottenere:
, si poteva ottenere:
![\begin{displaymath}
s'_{P}=T_{P}\times[f(x,y+\Delta)+a(x,y+\Delta,t')] \,\,
\end{displaymath}](img35.png) |
(2.2) |
dove  corrisponde ad un tempo di osservazione vicino a t.
corrisponde ad un tempo di osservazione vicino a t.
Sfortunatamente tale tecnica ha due svantaggi:
- Le due immagini ottenute muovendo lo specchio secondario possono essere
affette da variazioni residue di background, dovute alle differenze termiche
tra le due configurazioni del telescopio.
In altre parole, la tecnica di chopping è equivalente ad una rapida
traslazione tra due differenti telescopi: (A) per la sorgente e (B) per il cielo.
Denoteremo con  la differenza residua tra i corrispondenti sfondi.
la differenza residua tra i corrispondenti sfondi.
- Per ragioni ottiche e meccaniche l'ampiezza di chopping è solitamente
inferiore a 60 arcosecondi, cioè non è possibile osservare una porzione di
cielo troppo lontano dalla sorgente di luce. Se il telescopio è molto
sensibile, o la sorgente ha dimensioni elevate, nel suo intorno si
rileverà una percentuale di luminosità molto alta, ovvero risulterà:
 .
.
In base a queste considerazioni la differenza  sarà data, in
generale, da:
sarà data, in
generale, da:
![\begin{displaymath}
\Delta s_{A}=(s_{P}-s'_{P})=T_{P}\times[f(x,y)-f(x,y+\Delta)+\Delta a_{AB}] \,\,
\end{displaymath}](img57.png) |
(2.3) |
dove con  si indica che la sorgente è stata osservata con il
telescopio (A).
si indica che la sorgente è stata osservata con il
telescopio (A).
Per eliminare il fattore  , viene utilizzata una tecnica particolare
chiamata nodding:
il telescopio viene puntato verso una regione differente del cielo, in modo tale che
la sorgente sia osservata con il telescopio (B); cioè risulta equivalente
ad una traslazione di
, viene utilizzata una tecnica particolare
chiamata nodding:
il telescopio viene puntato verso una regione differente del cielo, in modo tale che
la sorgente sia osservata con il telescopio (B); cioè risulta equivalente
ad una traslazione di  nella coordinata
nella coordinata 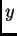 .
.
In questo modo, nel punto  si ottiene il segnale
si ottiene il segnale  e,
ripetendo l'intera sequenza, il risultato è:
e,
ripetendo l'intera sequenza, il risultato è:
![\begin{displaymath}
\Delta s_{B}=(s''_{P}-s_{P})=T_{P}\times[f(x,y-\Delta)-f(x,y)+\Delta a_{AB}] \,\,
\end{displaymath}](img59.png) |
(2.4) |
dove con  si indica che l'oggetto è stato osservato con il
telescopio (B).
si indica che l'oggetto è stato osservato con il
telescopio (B).
 rappresenta il segnale ottenuto con la tecnica descritta sopra.
rappresenta il segnale ottenuto con la tecnica descritta sopra.
Sottraendo l'equazione (2.4) dalla (2.3) si ottiene la cosiddetta
``chopped and nodded image'':
![\begin{displaymath}
g_{\Delta}(x,y)=\Delta s_{A}-\Delta s_{B}=Tp\times[-f(x,y-\Delta)+2f(x,y)-f(x,y+\Delta)] \,\,
\end{displaymath}](img60.png) |
(2.5) |
Tale immagine è indipendente dal fondo atmosferico e dal modello termico del
telescopio.
Se la distribuzione di luminosità della sorgente è compatta, cioè
 , allora il problema della ricostruzione di
, allora il problema della ricostruzione di
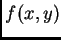 è risolto, altrimenti è necessario un metodo di ricostruzione
di
è risolto, altrimenti è necessario un metodo di ricostruzione
di 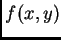 dall'immagine
dall'immagine 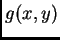 .
.
In generale, i telescopi giganti richiedono scale di pixel molto piccole e
utilizzano basse ampiezze di chopping, quindi si deduce che il caso in cui
 non è un caso standard.
non è un caso standard.




Next: Modellizzazione matematica
Up: Impostazione matematica del problema
Previous: Impostazione matematica del problema
Contents
Anna Custo
2002-02-05
![]() rappresenta la funzione di trasferimento del sistema,
rappresenta la funzione di trasferimento del sistema, ![]() è il segnale proveniente dalla sorgente cosmica e
è il segnale proveniente dalla sorgente cosmica e ![]() è il termine
di background.
è il termine
di background.
![]() e
questo risulta possibile solo se si conosce effettivamente il background
e
questo risulta possibile solo se si conosce effettivamente il background
![]() .
.
![]() arcosecondi nella direzione
arcosecondi nella direzione ![]() , si poteva ottenere:
, si poteva ottenere:
![]() sarà data, in
generale, da:
sarà data, in
generale, da: