Faculty: Una-May O'Reilly
Current Student: Varun Aggarwal
Alumni: Wesley O. Jin
Status: Active, within EVO-DesignOpt and recruiting new students
Opportunities: UROP Fall-Winter '06-'07, M.Eng '06-'07, UAP '06-'07

WHY AND WHAT?

Filters are an important part of all communication systems, be it analog/RF or a digital implementation. The first step of filter design is filter approximation, where the designer chooses a transfer function from one of the classical approximation functions, i.e. Butterworth, Elliptic or Chebyshev. In the early and mid 1900's, these approximation functions were revolutionary in facilitating design. Given specification in frequency domain magnitude response (ω_s, ω_p, A_max, A_min) and an objective, the designer could choose one of the approximations and the respective coefficients from a table of values according to the order. For instance, a Butterworth approximation is used if the designer's objective is maximum flatness (least magnitude error near ω=0) and a Bessel approximation is chosen for maximum phase linearity. In each choice, however, the designer is making a tradeoff. For example, a Butterworth approximation sacrifices on specificity of the filter to ensure maximum flatness. This is problematic because usually the designer generally has more than one design objective in mind. Additionally, the choice of the design is influenced by time-domain characteristics such as peak overshoot and settling time. In these circumstances, choosing from among classical approximations, the designer is provided with sub-optimal (with respect to his objectives) options.

This project's goal is to provide the designer with the flexibility of choosing a filter that satisfies his design constraints and shows trade-off solutions with regard to performance objectives in both frequency and time domain. For example, the designer can ask to achieve maximal linearity in phase response and minimum peak-overshoot in trade with maximum flatness with a constraint on settling time.  Such design flexibility is not possible with classical filter design methodology. To this end, we have devised the OptimFilt framework.[1]

A related goal of OptimFilt is to aid the designer in choosing the order for the filter. A higher order implies higher area and power. A designer does not wish to choose a higher order unless it provides substantial improvement for the objectives the design. How does the designer know how much improvement will be derived by increasing the order? A goal of OptimFilt is to inform the decision of the designer by flowing information bottom-up throughout the design flow. It will provide the designer with a visualization of the performance space of filter for each order. This will enable the designer to choose the optimal order appropriate to the trade-off issues.

This approach of modeling feasibility space bottom-up [3] will enable optimal System-Level design. Given the feasibility space, the designer can then use and adjust system level performance specifications to choose the order and the trade-off point for the order. This will circumvent the sub-optimal solutions created by conventional design flow that rely on experience and the guesses of the designer. These approaches will yield filter approximations which are optimal for filter performance objectives and for the crucial objectives of power and area. To address the low power criteria effectively, we include Q as an additional minimization objective in OptimFilt.

We plan to conduct real-world case studies to assess the usefulness and performance of the OptimFilt tool.

HOW?

We have an end-to-end system based on PSO, which can accept multiple constraints and objectives and gives an optimal filter realization according to it. The first paper on this approach is under review [1]. We showed how our approach beats convex optimization techniques like Sequential Quadratic Programming [2] by making a one-to-one comparison. For illustration, the time response of a Butterworth, SQP-tuned and PSO-filter are shown in Figure 1. The filters were tuned for maximal phase linearity and minimum peak overshoot.

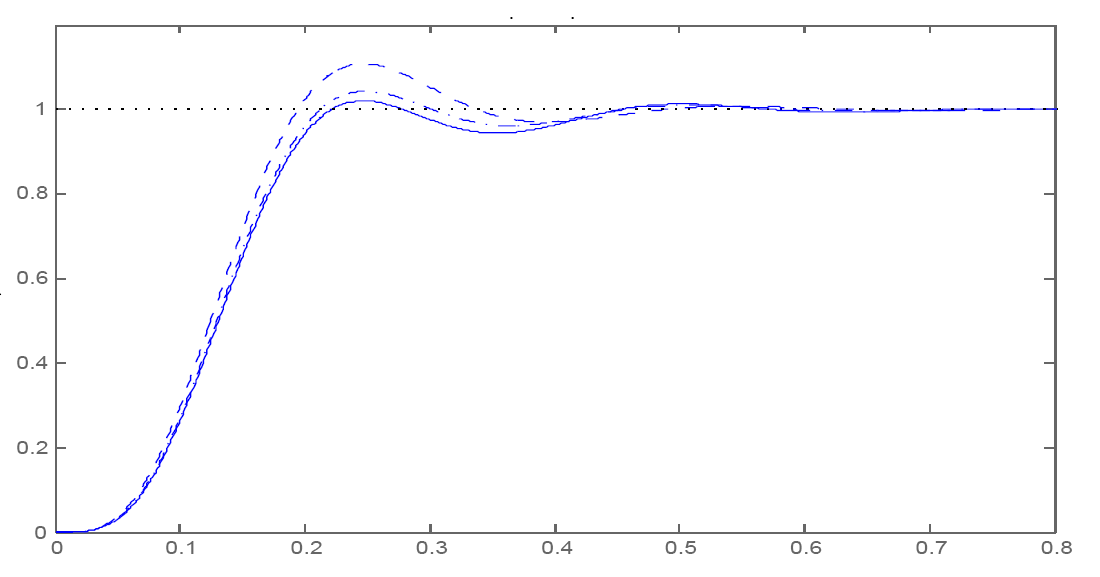
Figure 1: Step Response for Butterworth (- -), SQP (-.) and OptimFilt Solution (line). X-axis: time(s), Y-axis: Magnitude

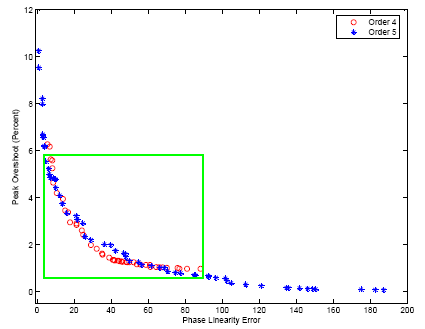
Figure 2: Performance Space for all-pole filter with respect to phase linearity and peak overshoot for order 4 and 5.

We have just developed an algorithm which enumerates trade-off solutions across multiple objectives. This is our first step towards performance space modeling of filter design. In Figure 2, we show the performance of a filter on the objectives of phase linearity and peak overshoot for orders 4 and 5. If the designer wants a design in the trade-off space bounded by the rectangle, there is no advantage to using a higher order. However, a higher order would be advantageous if the design is in the space outside the rectangle. Now the order decision can be made comfortably while knowing a quantitative measure of performance improvement.

Design of reliable algorithms to be able to do this for multiple objectives is underway. Objectives which address circuit realization issues (for instance, low sensitivity of filter performance with component value variation) will also be included in these algorithms. We will address real-world case studies to assess the usefulness and performance of the algorithms.

References:

[1] V. Aggarwal, M. Mao and U. M. O'Reilly. Filter Approximation Using Explicit Time and Frequency Domain Specifications. Under Review, (Available on Request)

[2] N. Damera-Venkata and B. Evans. An automated framework for multicriteria optimization of analog filter designs. In IEEE Trans. Circuits Syst. II , Vol. 46, pg 98190 Aug. 1999.

[3] G. G. E. Gielen, Trent McConaghy, Tom Eeckelaert. Performance space modeling for hierarchical synthesis of analog integrated circuits. Design Automation Conference, pp. 881-886, 2005