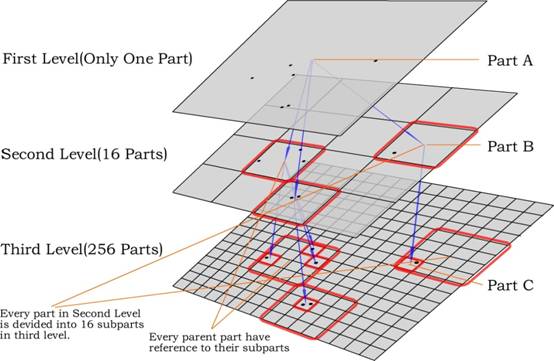
Macro To Micro
Model
This project is supported student research project(SRP) of SCUT.
We
introduce a generally applicable algorithm model named Macro-to-Micro Model (M
Generally, Using M
1)
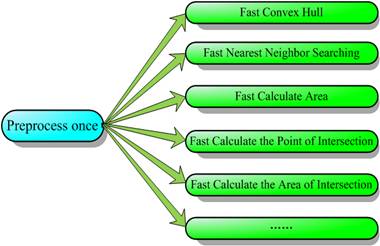
Preprocessing: Data set should be divided into a number of similar
partitions through Macro to Micro levels. This processing is similar to human
being's behavior when developing the view of the problem.
2)
Query: From macro to micro, shrink the search space at
every level and use the algorithms based on M
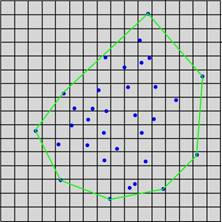
Nearest Neighbour Searching in Planar
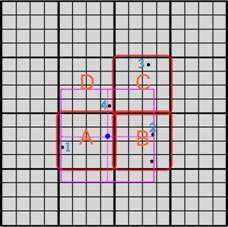
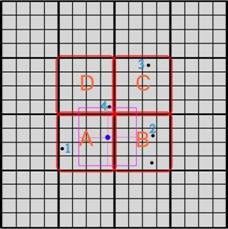
Illustration example:
1. Querying part A, current
nearest point 1 is found.
2. Searching bound shrinked,
found current nearest point 2 in part B.
3. Querying Part C, Searching
bound no change.
4. Searching bound shrinked
again and all area intersected has been searched, found point 5 is global nearest
point.
Step 1
Step2
Step
3
Step
4
More detail about this algorithm can be found in our paper: A_New_Nearest_Neighbour_Searching_Algorithm_based_on_M2M_Model.pdf.
Convex Hull Algorithm
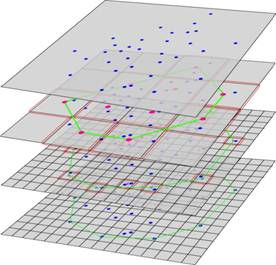
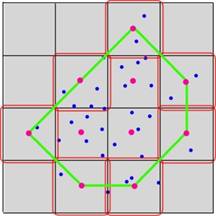
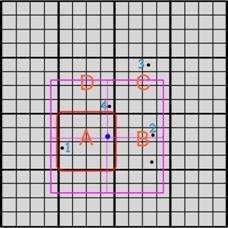
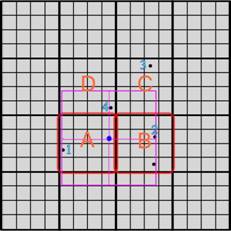
Our algorithm will firstly get all the
parts containing at least one point and compute the convex hull of the centers
of those parts in topmost level, which is shown in Figure 3. Secondly, all the
subparts of the parts which are in the Center-Hull will be considered in the
next level. In the next level, the algorithm will check all the parts handled
by the last level and similarly find out all the parts containing at least one
point, then compute the Center-Hull of those parts, as shown in Figure 4. It is
worthwhile to notice that our algorithm only concerns the centers of the parts
handled by the last level and containing at least one point, which leads to a
great shrink to the searching space. The algorithm repeats similar processing
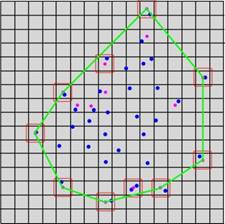
in the following levels, until reaching the bottom level. In the bottom, the
algorithm will consider not just the centers of the parts handled by the last
level but all the points contained in those parts, and output the convex hull
among considering points, as shown in Figure 5.
|
|
|
|
Figure 2: The point set |
Figure 3: The Center-Hull in the top level |
|
|
|
|
Figure 4: The Center-Hull in the next level
|
Figure 5: After several levels computing,
the algorithm returns the final convex hull in the bottom level |
More detail about this algorithm can be
found in our paper :A
New Randomized Parallel Dynamic Convex Hull Algorithm based on M2M model.pdf
and The proof of Correctness
Of M2MCH.pdf.
Path Finding algorithm
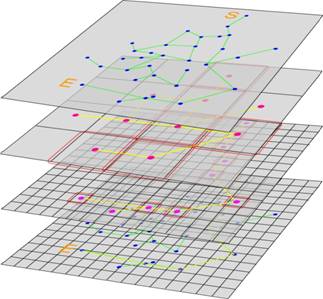
Path Finding algorithm based on M2M is
different from two kinds of algorithm above can always find the optimal
solution, but it still very useful in many application.
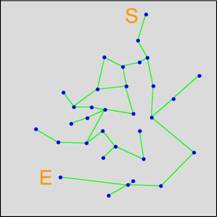
Illustration example:
1. S is the Start point and E is
the end point, our task is finding a path between S and E.
2. Searching the path in the top
level extract the solution path as the next level input.
3. Searching the path among the
parts in the next level according to the last solution.
4. Searching the path in the
bottom level, then output the solution.
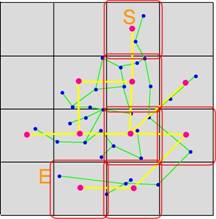
Step 1 Step 2
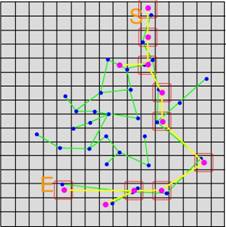
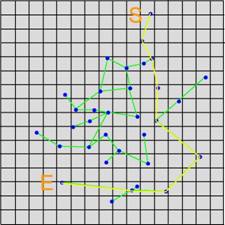
Step
3 Step 4
The advantage of M2M model
Compared with conventional algorithms, Convex hull algorithm
based on M
1)
High parallelism: The preprocessing to setup a M
2)
Dynamic structure: The operation of M
3)
Preprocessing
sharing:
The algorithms based on M
4)
Trade-off
between the efficiency and the precision: As with other M
5)
Trade-off
between time efficiency and space cost: The parameters of M
Other application of M2M model
With the help of M