http://people.csail.mit.edu/jaffer/Geometry
	Geometry

Topological Computer Graphics Ink Marbling

Nano Cellular Automata

Multidimensional Space-Filling Curves Color Space Dimension Reduction

Packing Pyramids

Extrapolating the Limit

Number Theory: f(Z x Z) = N?

Why Musical Scales Work

Display Calibration Image Size Check

Conventional computer graphics primitives are overwhelmingly based on straight lines. NURBS and other patches decimate surfaces into triangles for rendering. And what about the field of topology, where straight lines and flat surfaces are degenerate cases? Topological Computer Graphics creates some new graphics primitives entirely about curvature, differentiability, and continuity.

Multidimensional Space-Filling Curves are generalizations of the two-dimensional curiosities constructed by Peano and Hilbert in the late 1800s. Although filling (hyper)cubic volumes, the space-filling curves are infinitely wiggly -- continuous everywhere while differentiable nowhere. They can be seen as an entirely different approach to nonlinear primitives.

Color spaces are bounded, 3-dimensional volumes. Color Space Dimension Reduction uses space-filling curves to organize color spaces for creating color catalogs. It is surprising when novel counterexamples find practical use.

Packing Pyramids compares volumes created by rising-factorial sums with cubes.

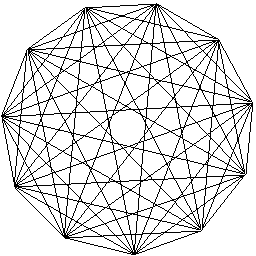One problem with the straight computer graphics lines is that they are not straight when inclined! Staircasing is a prominent artifact in most rendering systems.

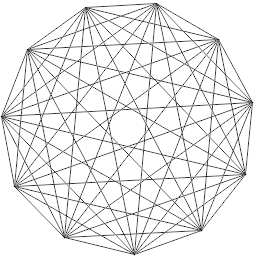The image to the right, drawn with anti-aliased line primitives, looks much smoother than the image above it. The degree to which lines are perceived as smooth depends on the computed and actual display gamma, a property of the display hardware.

If the quality of anti-aliased images is sensitive to display gamma, does this make them a good way to measure it? A chart of complete graphs at various computed gammas does function as a gage. But the highly compact chart in Display Calibration allows finer distinctions in gamma to be discerned with the unaided eye. It uses a cleverly designed 11-level dispersed screen which should be optimal for that number of levels.