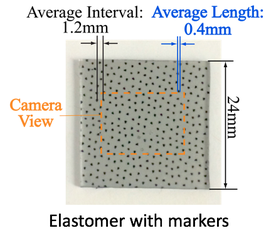
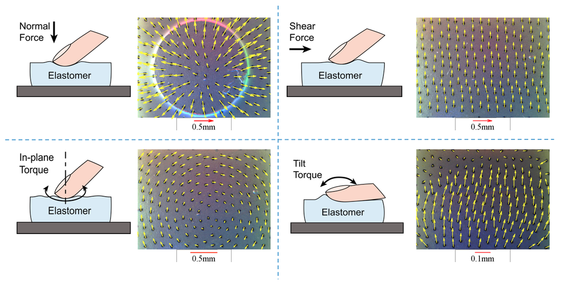
Inferring contact force, shear and slip with markers on GelSight
In this project, we paint markers on the GelSight surface and track their planar displacement in the image. We found that the marker displacement represents the contact force. On one hand, the pattern of the movement field is related to the force type; on the other hand, the magnitude of the displacement is in the portion to the force magnitude. The markers are very sensitive to small forces.
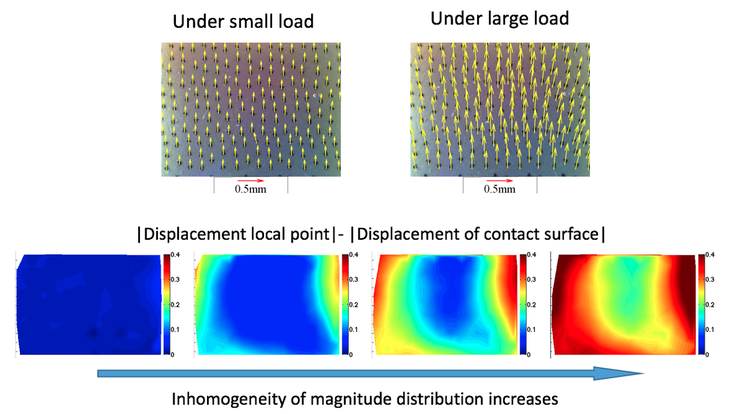
The markers are also good to tell shear and slip states, which can hardly be inferred from contact geometry. We found that when shear force is large, slip is likely to occur soon, and the contact is in a state of `partial slip', which means the slip already occurred at the border. The degree of partial slip, and how likely the slip is going to occur, can be measured by the homogeneity of the magnitude distribution of the marker motion. An example is shown as the following:
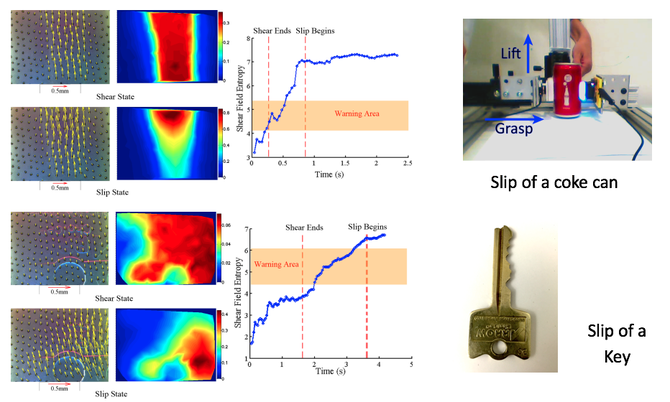
We use entropy to describe the degree of slip is likely to occur. In the experiment, we use a 2-finger mechanical jig to hold an object (either a coke can or a key), and a human trying to lift the object from the hold. In the process, the shear force grows, and slip occurred at the end. The following figures compared the GelSight image in the beginning stage, and finishing stage, and how the entropy in the contact area changes through the process.
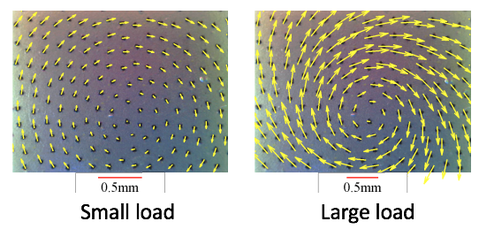
The rule also applies to rotational load: when the rotational torque is large, rotational slip would occur, and the border area slips first. The inhomogeneity of the rotation angle distribution is a good indication of how rotational slip is likely to occur. The following figures shows the marker displacement fields when the rotational load is small and large:
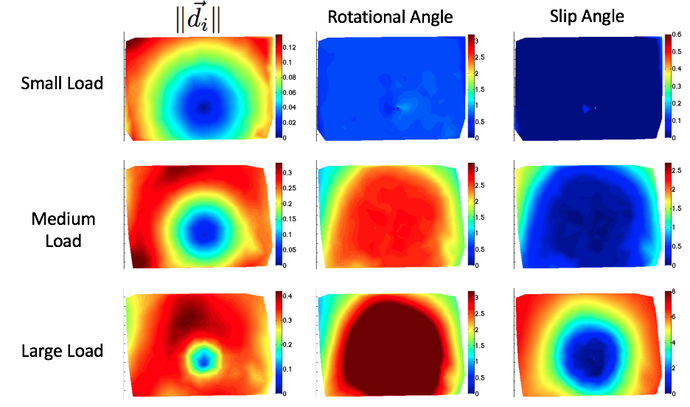
In the following figure, we draw the heat map of the magnitude distribution: the figures in the left column compares the motion magnitude of the markers, the figures in the middle column compares the rotational angles of the markers around the rotational center, the figures in the right column shows the subtraction result of the rotation angle of the contact surface and the angle of the markers.