http://people.csail.mit.edu/jaffer/SimRoof/SolarScreen
	SimRoof: Solar Screen

• Introduction
• Sites
• Weather
• Net Radiative Transfer
• Lambertian Perfromance Limits
• CoolRoof
• Roof Convection
• Solar Screen Model
  • Definitions
  • Thermal Conductance of Plane Air Space
  • Bounce Gain
  • Equilibrium
• Solar Screen Performance
• Thermal Infrared Optics (footnotes and supplemental information)

A solar screen is a film of material between the roof and sky enclosing an airspace. The screen temperature can be higher or lower than the roof temperature, depending on conditions.

A heated screen adds an additional downward thermal infrared source to the simulation. The distance between the screen and the roof (emitter) is small enough that the enclosed air doesn't interact with radiation. That means that interactions between the roof and solar screen do not need high spectral resolution, and can be computed after the NIRT model is generated.

Definitions

Thermal Conductance of Plane Air Space

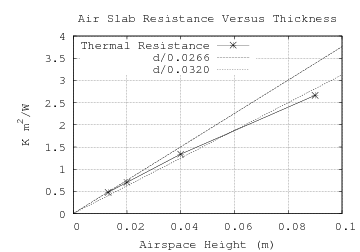
Because the roof is at or below ambient temperature, there is insignificant upward convection to the screen. That leaves radiation (treated separately) and (downward) conduction. From 1997 ASHRAE Fundamentals Handbook (SI) chapter 24 Table 3 "Thermal Resistances of Plane Air Spaces" we can extrapolate the non-emissive downward conductivity for 13 mm, 20 mm, 40 mm, and 90 mm airspaces (left graph). The graph on the right shows the curve connecting the four non-emissive resistances (reciprocal of conductance). The d/0.0266 line is the theoretical non-convective resistance; but d/0.0320 is a better fit.

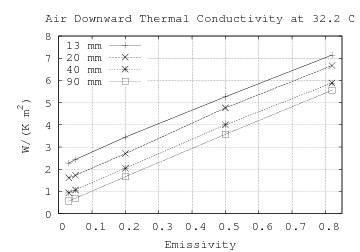
Let the airspace-conductance k=0.032/d. At d=0.250 m, k=0.128 W/(m²·K).

Bounce Gain

Because the terms have values between zero and one, the sum converges to:

Equilibrium

		sky IR down	−up IR	airspace IR	conduct	solar	convect
roof-heat-gain:		( N(TA) + M(TA)	− M(TB) ) · εB · τS	+ ( M(TS) − M(TB) ) · (εB · εSB)	+ (TS − TB) · k	+ IB
Screen thermal balance:	0 =	( N(TA) + M(TA)	− M(TS) ) · εST	+ ( M(TB) − M(TS) ) · (εSB · εB)	+ (TB − TS) · k	+ IS	− (TS − TA) · h(v)

The goal is to find the roof-heat-gain (or loss). But roof-heat-gain depends on T_S, the only free variable in the screen-thermal-balance equation. If T_A=T_B, then the balance equation can be written:

( M(TS) − M(TA) ) · (εSB · εB + εST) + (TS − TA) · ( h(v) − k ) = N(TA) · εST + IS

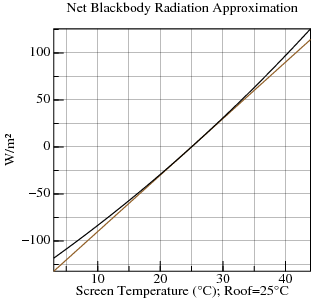
M(T)=σ·T⁴: The tangent of M(T) at T_A is 4·σ·T³. At 25°C, the slope is 6.012. Replace M(T_S)−M(T_A) with its linear approximation:

We can then solve for T_S:

For the general case, the first-order Taylor approximation of M(T_S)−M(T_B) around T_A is:

Then:

Yielding:

See simulations of several solar-screens.