http://people.csail.mit.edu/jaffer/SimRoof/NRT
	SimRoof: Net Radiative Transfer

• Introduction
• Sites
• Weather
• Net Radiative Transfer
  • Simulation Inputs
    • Solar Absorption
    • Upward Thermal Radiation
    • Downward Thermal Radiation
  • Simulation Strategy
  • Lambertian Model for the Tropics
  • Lambertian Model for Southwestern US Deserts
• Lambertian Perfromance Limits
• CoolRoof
• Roof Convection
• Solar Screen Model
• Solar Screen Performance
• Thermal Infrared Optics (footnotes and supplemental information)

99% of the sun's radiance is at wavelengths shorter than 4 µm; while 99% of a 25°C blackbody's radiance is at wavelengths longer than 4.8 µm. So we can consider solar and thermal radiance separately. The three quantities to compute for a prototypical square meter of roof are:

Solar Absorption

The direct and indirect solar radiation. Most of this radiation is at visible wavelengths.

Upward Thermal Radiation

The blackbody infrared radiation emitted by the roof.

Downward Thermal Radiation

This is the difficult part. Thermal infrared radiation is absorbed and re-emitted by water vapor at elevations throughout the troposphere. The spectrum of the re-emitted radiation depends on the temperature (and hence the altitude) of the water vapor emitting it.

More problematic may be emission and scattering by clouds. The sections Weather, Cloudless Sky, and Cloudy Sky discuss these models.

Kirchhoff's Law of Thermal Radiation dictates that in every band, a body must emit the same proportion of thermal radiation as it absorbs. The Infrared Scattering page establishes that thermal-infrared radiation is not significantly scattered by clear air. Without scattering (or reflection), the correspondence between absorption and emission is of interest because it allows the use of atmospheric transmission data to calculate emissivity of cloudless atmosphere: That portion of mid- and far-infrared radiation which isn't transmitted is absorbed.

The Infrared Scattering by Water Clouds page argues that water and ice clouds can be treated as (opaque) blackbodies. The infrared transparency of the atmosphere between the ground and cloud-base is no different than that for cloudless sky. The cloud-base is modeled as the remaining moisture in a layer of liquid at the cloud-base height.

In the tropics, ice clouds occur at high altitudes. They will play a role only if there are not opaque clouds below them. Because high ice clouds are at cold temperatures (as estimated by the lapse-rate), treating them as cloudless sky will not introduce large errors.

Simulation Inputs

The angle-dependence is the angle from zenith. Angle-dependent optical functions allow modeling of the aperture-restriction discussed in Optics for Passive Radiative Cooling.

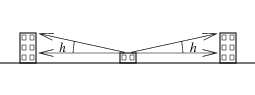Angle-dependent optical functions can model when buildings or terrain obstruct the horizon. This can be done in a manner analogous to the way clouds are treated: for each angle near the horizon, the obstruction percentage of the incoming radiation comes from a blackbody at a temperature at or above ambient through the average distance to the obstructions. During the day, the temperature of obstructed horizons is greater than ambient due to solar heating. Introduced is a solar-temperature-gain (stg) parameter which is the temperature increment (°C) per 1000 W of TMY3 Global-Horizontal-Irradiance (ghi). For an angle h above the horizon (π/2−h from the zenith), the solid angle to the horizontal plane is π·sin²(h)=(π/2) (1−cos(h)). For a given solid angle γ, the h having the same solid angle is cos^-1(1−(2/π)·γ).

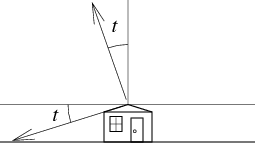If the roof has a small tilt t, then the airmass over most of the hemisphere is not much different than for a horizontal roof. The difference is that a spherical wedge between the plane of the roof and the horizontal plane receives thermal radiation from the ground or buildings. The solid angle subtended by tilt angle t is 2t (radians).

Lambertian Roof	Angle Dependent	Angle and Wavelength Dependent
The simplest configuration is a horizontal, Lambertian surface under a full hemisphere of unobstructed sky.	Aperture restricted to a cone around the zenith; also handles obstructed horizons and small roof tilts (less than 15°).	Spectral optical function, horizon obstructions, and daylight spectra must be compiled into the NIRT array, making it specific to a single configuration.

Solar Absorption

Upward Thermal Radiation

Downward Thermal Radiation

All the inputs for computing upward-thermal-radiation are also inputs for computing downward-thermal-radiation; and computing upward-thermal-radiation is an order of magnitude simpler than downward-thermal-radiation. So the upward and downward thermal radiation computations can be combined.

troposphere.pdf gives the mathematical details of the thermal radiation calculation.

Simulation Strategy

• ceiling-height,
• dry-bulb temperature,
• precipitable-water, and
• atmospheric-pressure.

For Lambertian roofs (described in Simulation Inputs), a single table can be used to simulate any TMY3 (whose values are within its range). For rotational-symmetry cases a single table which stores values for each ray-angle can be used, 5850 values in the example below. For the general-case (wavelength-dependent emissivity), a table must be calculated for each emissivity-function. But that table is valid for any TMY3 (whose values are within its range).

• Lambertian Model for the Tropics
• Lambertian Model for Southwestern US Deserts