http://people.csail.mit.edu/jaffer/CNS/DIMPA
	The Distribution of Integer Magnitudes in Polynomial Arithmetic

Motivation

Straightforward polynomial arithmetic algorithms tend to generate intermediate polynomials with large numerical coefficients. Bignum (arbitrary-precision) arithmetic is needed to manipulate other than contrived equations.

Examination of the sizes of integers occurring in actual symbolic algebra calculations clearly directs optimization efforts toward fixnum and mixed fixnum-bignum operations.

Apparatus

• 448.974.MHz Intel Pentium II (Deschutes)
• RedHat-7.3 Linux 2.4.18-18.7.x i686
• 2003-01-01 Development version of SCM 5d7
• 2003-01-01 Development version of SLIB 2d5
• 2003-01-01 Development version of JACAL 1b2
• gnuplot 3.7.1 (from gnuplot-3.7.1-17.src.rpm)
• scheme program intdist.scm in the jacal directory
• gnuplot script intdist.plt in the jacal directory

Procedure

• cd to the jacal directory
• scm -l intdist.scm
• Graphs are written in the jacal directory:

  "logdist.png"

  Graph of log₂(1+count) versus bit-length of integers.

  "intper.png"

  Expanded Graph of:

  • the count (relative to total) for each bit-length; and
  • the sum of counts for all longer bit-lengths.

Method

• The intdist.scm program instruments the Scheme primitives *, +, -, /, GCD, LCM, MAX, MIN, MODULO, QUOTIENT, and REMAINDER to increment HISTARRAY[btln] where btln is the number of bits requried to represent the absolute-value of the result of the primitive operation.
• The program then starts jacal and runs its regression suite "test.math".
• The instrumentation wrappers are removed from the Scheme primitives.
• Capured data is written to files:
  • "logdist.dat"
  • "intper.dat"
  • "per.dat"
• (system "gnuplot intdist.plt") creates the JPEG graphs.

The JACAL regression suite spends most of its running time factoring polynomials. Although factoring uses modular and p-adic algorithms, the polynomial GCD code does not. The square-free factorization (a preliminary to modular factoring) uses GCD heavily. I suspect it is responsible for the bulk of the larger integers.

Measurements

The low number of `/' calls is because `/' can return inexact numbers. QUOTIENT always returns exact numbers; hence it is more suitable for polynomail ring arithmetic.

Histogram of Integer Magnitudes

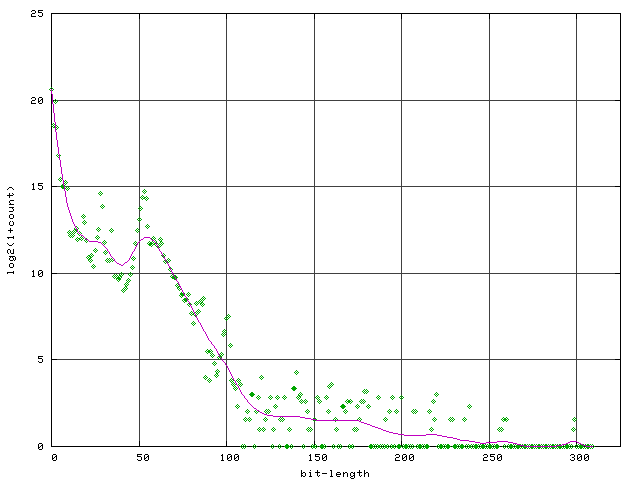
At 1623699 returns, the integer zero is the most frequent. 2 and 3 (and -2, -3) are next highest with 1006600 returns. The number 1 (and -1) trails with 375121 returns.

From zero, each 50.bits of additional bit-length reduces frequency by a factor of roughly 500. Above 120.bit, 50.bits of additional bit-length reduces frequency by a factor of 2.

Graph of relative frequencies versus bit-length

• Over 92% of the returned integers are less than 1024.
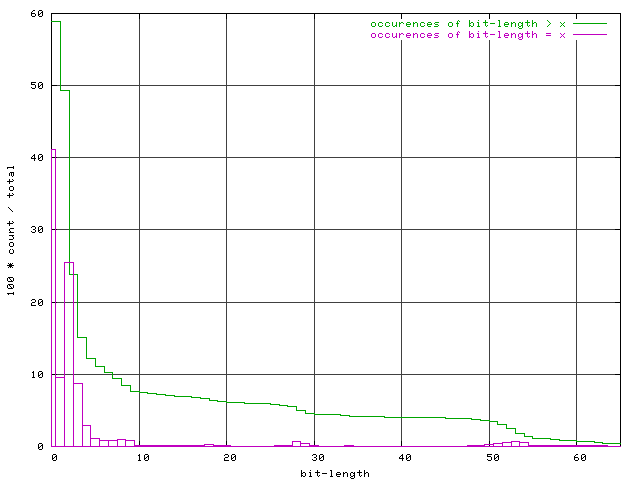
• 95% of the integers are less than 30.bits, fitting in SCM's INUM (immediate-integer) type.
• Only 5% of operations return bignums (in SCM).
• Fewer than 0.5% of operations return bignums larger than 63.bit.

Discussion

Efforts to optimize speed will bear the most fruit when directed to the fixnum operations representing the vast majority of arithmetic calls. Tests for zero should be placed as early as possible in each routine, since roughly 40% of calls will receive a zero argument.

Nonzero fixnum-fixnum operations are next in priority to process quickly; followed by fixnum-bignum combinations. SCM also treats integers only two "digit"s long (32-bit) specially to reduce memory allocation.

That a non-integrated multi-precision package will necessarily have poor performance is not news to the authors of GNU MP 4.1. In GNU MP 4.1 Efficiency they write:

Small operands

On small operands, the time for function call overheads and memory allocation can be significant in comparison to actual calculation. This is unavoidable in a general purpose variable precision library, although GMP attempts to be as efficient as it can on both large and small operands.

Numerical naivete apparently motivated developers of Guile, which is descended from SCM, to replace SCM's integrated arithmetics with an external package. Guile uses GNU MP:

I deleted all code belonging to the old bignum implementation and replaced it with calls to some older GMP...

On my PII 266 with 64MB it now computes (factorial 10000) in about two seconds, if no garbage collection occurs. If gc is activated however, guile performs the calculation within 200KB and calls gc several times. The whole thing takes about 25 seconds (!), but this is still twice as fast as the old implementetation. (I do not garantee for these figures).

(factorial 10000) is a 118459.bit number. Numbers that large are of number-theoretical interest only. For example, secure encryption keys are currently 1024 bits. Public keys 100 times wider would take 10000 times longer to compute; not practical for Internet shopping.

That such a large number was necessary for FFT multiplication to prevail over O(b²) multiplication is high praise for the SCM implementation.

Conclusion

The large reduction in frequency of occurrence versus bit-length means that small improvements in asymptotic running times for exotic bignum algorithms would bring negligible benefit in running this computer algebra program.

The strategies of tight integration of bignum code into SCM's numerics and emphasis on optimizing arithmetic for small numbers seem the best approach to providing numerical speed in support of JACAL.