

| http://people.csail.mit.edu/jaffer/cool/CoolRoof |
Cool Roof |
The Cool Roof Rating Council (CRRC) "is an independent, non-profit organization that maintains a third-party rating system for radiative properties of roof surfacing materials." Solar reflectance and thermal emittance are measured and certified for roof products both new and after 3 years of outdoor exposure at a CRRC Approved Test Farm.
About their Product Rating Program:
The CRRC administers a Rating Program in which companies can label roof surface products with radiative property values. The CRRC does not set a minimum definition for "cool", the CRRC simply lists the measured radiative property values on our Directory. Any roofing product can be tested as long as it is in compliance with the Product Rating Program Manual (CRRC-1). A product's placement on the Directory does not mean that the product is "cool" as defined by any particular code body or program.
All radiative property testing is conducted by accredited testing laboratories... Solar reflectance can be measured in accordance with ASTM test methods C1549, E1918,
E903, and CRRC-1 Method #1: Test Method for Certain Variegated Products. Thermal emittance is measured in accordance with ASTM C1371. For aged ratings, product samples are exposed for three years at the CRRC Approved Test Farm. Product ratings are verified periodically through the CRRC's Random Testing Program.
The CRRC's two measurements (solar reflectance and hemispheric thermal emittance) do not, by themselves, indicate the energy savings or suitability of a cool-roof product, but must be evaluated in the context of climate data[SimRoof]. For example, in temperate zones, highly reflective and emissive roofs can increase the cost for winter heating more than they reduce the cost for summer cooling!
| Sorted by \ Subset | All | Bright White | Granul | r3≥0.8 e3≥0.8 |
|---|---|---|---|---|
| Initial Solar Reflectance | 1259: 0.93-0.06 | 356: 0.92-0.27 | 23: 0.84-0.31 | 11: 0.92-0.82 |
| Third-Year Solar Reflectance | 942: 0.87-0.07 | 235: 0.87-0.24 | 11: 0.70-0.27 | 11: 0.87-0.80 |
| Initial Thermal Emissivity | 1259: 0.99-0.05 | 356: 0.99-0.78 | 23: 0.97-0.79 | 11: 0.91-0.87 |
| Third-Year Thermal Emissivity | 942: 0.99-0.10 | 235: 0.97-0.58 | 11: 0.97-0.82 | 11: 0.93-0.84 |
As of 2010-05-01, there were 1259 low-slope materials in their database. The range of initial solar reflectances was 0.93 to 0.06.
Considering only the 356 "bright white" products, the range was 0.92 to 0.27. Only one product had reflectance above 0.82 after 3 years; seven had reflectance of 0.8 or better after 3 years.
The range of initial thermal emissivities was 0.99 to 0.05, Without the bottom three (e=0.05 "Modified Bitumen"!?) and one with e=0.27, the range was 0.99 to 0.33. The string "granul" occurred often (23 times) among the descriptions of the high-emissivity materials, the lowest granular emissivity being 0.79. The granulars had initial solar reflectances of 0.84 to 0.31, although only one had reflectance below 0.65.
Among bright-whites, the initial thermal emissivity ranged from 0.99 to 0.78. After 3 years, the thermal emissivity ranged from 0.97 to 0.58, although there were only 3 below 0.79 and third-year results were pending for 1/3 of the products.
Among the bright-whites, the granular products ranked only in the bottom half when sorted by third-year reflectivity (0.61 to 0.27). Among the granulars, there was only one with a third-year reflectivity of 0.70; the rest were at or below 0.61; about half were pending.
The fourth column shows that there were only 11 products with third-year reflectance and emissivity of 0.80 or greater. None of these products had "granul" in its description.
There was only one product with third-year reflectance and emissivity greater than 0.85.
A photon striking flat sheet of opaque material is either absorbed or reflected. Now consider a photon striking a very bumpy sheet of opaque material. It may be absorbed or it may be reflected, but, if reflected, it may strike the material a second time. This reduces the effective reflectance and increases the effective absorbance of the material. Kirchhoff's Law of Thermal Radiation establishes that in every band, a passive body must emit the same proportion of thermal radiation as it absorbs. Thus, creating a rough or granular surface tends to increase thermal emissivity and decrease solar reflectance compared with a smooth flat surface.
In most regions, dust will accumulate on a roof. Dust will not usually be very solar-reflective; so it reduces solar-reflectance of high reflectance surfaces. All of the high solar-reflectances in the table show degredation with age.
Dust on a surface makes it bumpier; so there is little degradation of thermal-emissivity with age. The thermal-emissivity of some materials even improves with age.
There is a tension between high thermal-emissivity and high solar-reflectance. Materials do not simultaneously excel in both metrics over the long term.
Which is more important to performance, solar-reflectivity or thermal-emissivity? The solar radiation absorbed is the product of the incident solar-radiation and 1 minus the solar-reflectivity. An improvement in solar-reflectivity from 0.80 to 0.90 halves the absorbed solar-radiation! In contrast, an improvement from 0.80 to 0.90 of thermal-emissivity increases the thermal-radiation by only 11%. Therefor, solar-reflectivity is an order of magnitude more important than thermal-emissivity in choosing a cool-roof.
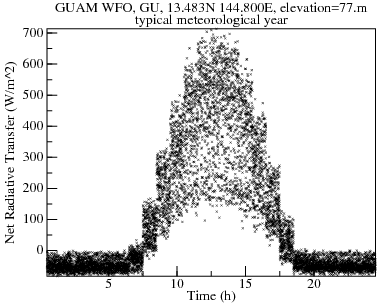
To the right is a net-radiative-transfer plot for my guess as to the parameters for grey asphalt shingles: a solar-reflectivity of 0.25 and 0.83 emissivity. Its peak heating is only 24% better than the completely-absorbing roof in Tropical Lambertian Perfromance Limits.
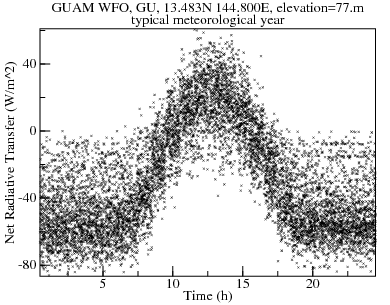
Among the registered cool-roof materials, there is one each of materials with initial solar-reflectivities of 0.93, 0.92, 0.91; and nine materials with an initial solar-reflectivity of 0.90, most of which have initial emissivities of 0.87. This simulation is of the initial properties 0.90 and 0.87, and situated on the tropical island of Guam.
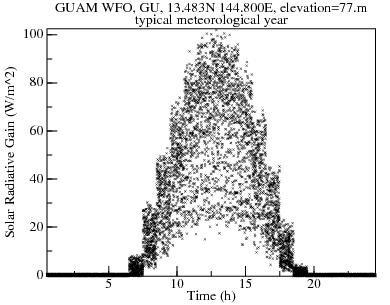
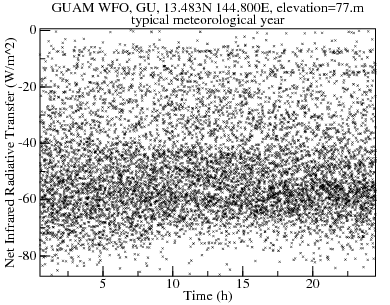
The solar heat gain is strongly dependent on time-of-day; but net-infrared-radiative-transfer is only weakly dependent.
| 
|
| 
|
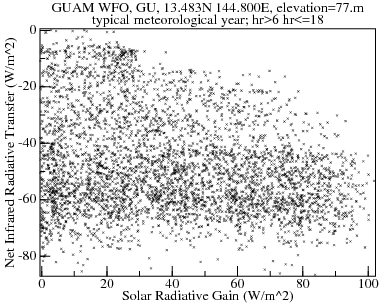
Compared to the hypothetical asphalt-tile roof above, peak heat gain is reduced by more than a factor of seven (725 W/m2 to 103 W/m2)! Most of the reduction is due to the CoolRoof being much more reflective (90% vs 25%). Radiative cooling is responsible for reducing the peak solar-radiative-gain of 100 W/m2 to a net-radiative-transfer below 60 W/m2. A plot of daytime net-infrared-radiative-transfer versus solar-radiative-gain shows that the highest solar gains are accompanied by at least moderate radiative cooling. This is probably because high solar gains require fairly clear skies, which support radiative cooling.
|
This simulation used SimRoof's Lambertian model, which is basic. To simulate tilted roofs and obstructed horizons, the angle-dependent SimRoof model should be used.
Solar-reflectivity is the primary determinant of cool-roof performance.
Solar heat gain is somewhat correlated with radiative cooling; the worst case radiative cooling (0 W/m2) does not happen simultaneously with the highest solar intensities.
In simulations of tropical climates, the top ranking cool-roof products significantly reduce peak solar heat gain both through reflecting solar radiation (90%) and radiative cooling (40 W/m2).
|
I am a guest and not a member of the MIT Computer Science and Artificial Intelligence Laboratory.
My actions and comments do not reflect in any way on MIT. | ||
| Radiative Cooling in Hot Humid Climates | ||
| agj @ alum.mit.edu | Go Figure! | |