|
| http://people.csail.mit.edu/jaffer/SimRoof/ThermalOptics |
SimRoof: Thermal-Infrared Optics |
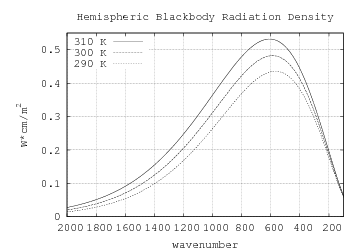Planck's
Blackbody Formula gives the maximum spectral density of power
radiated by a blackbody,
"a perfect radiator which absorbs all radiation incident upon it".
To the right is a graph of the Planck formula for temperatures
spanning 98% of the weather experienced by the 19 tropical locations
in the TMY3 data-set.
| temperature | total radiated power | |||||
|---|---|---|---|---|---|---|
| 310 K | = | 37°C | = | 98°F | → | 524 W/m2 |
| 300 K | = | 27°C | = | 80°F | → | 459 W/m2 |
| 290 K | = | 17°C | = | 62°F | → | 401 W/m2 |
Materials which transmit most room-temperature thermal-infrared radiation are rare: anhydrous salt crystals and unweathered polyethylene. Even a desert atmosphere obstructs so much thermal-infrared that the cooling powers given above cannot be approached at sea-level.
Electrically conductive metals reflect infrared radiation. Building materials which reflect most thermal-infrared are termed low-emissivity, and are valued for retaining interior heat or rejecting exterior heat.
Semiconductors can be conditionally reflective. If photons with higher than the band-gap energy impinge on a semiconductor, they will be absorbed and generate carriers, thereby causing the (lower-energy) infrared radiation to be reflected. This is the case for all but the highest bandgap semiconductors.
In particular, conductive metals in granular form act as high-IR dielectrics, as detailed in Granular Metal Films. For thermal-infrared applications, granular-metal composites may be the only practical source of high refractive-index dielectrics.
Thus the blackbody radiative flux through an aperture can be no greater than that produced by a blackbody at the same temperature having that aperture as its surface.
Therefore, blackbody radiation cannot be concentrated by any arrangement of mirrors. The rate of cooling is limited by the smallest aperture through which the blackbody radiation all flows.
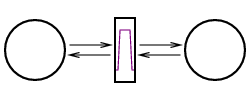
Now suppose that the filter passes radiation only in the 5 μm to 10 μm band, the object on the right is a perfect blackbody, and the object on the left emits only 35% of the (perfect) blackbody radiation in the 5 μm to 10 μm band. The blackbody on the right will emit 100% of the blackbody radiation in that band. If the object on the left absorbs more than 35% of of the impinging radiation in the 5 μm to 10 μm band, then there would be a net transfer of blackbody radiation to the body on the left, which would contradict the finding above. Similarly, if the object on the left absorbs less than 35% of of the impinging radiation in the 5 μm to 10 μm band, then there would be a net transfer of blackbody radiation to the body on the right, which would again contradict the finding above. Thus, in every band, a body must emit the same proportion of thermal radiation as it absorbs.
It seems reasonable that neither Rayleigh scattering nor Mie scattering would be involved in clear (infrared) skies because the air molecules are so much smaller than the thermal-infrared wavelengths.
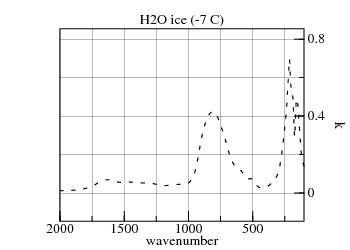
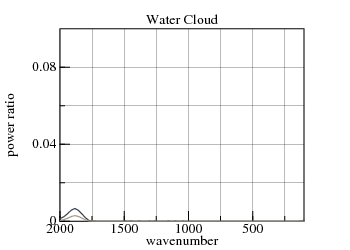
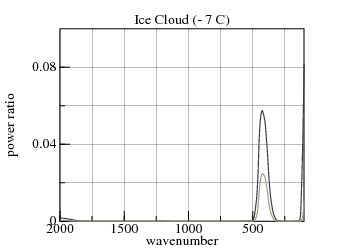
First consider small droplets. The refractive-indexes of water and ice have significant k>0 through their thermal ranges (4.5 μm to 40 μm):
| 
|
|---|
| 
|
|---|
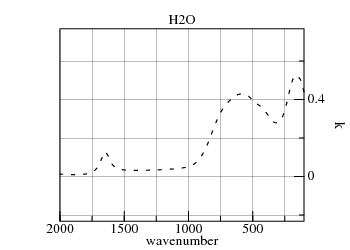
Imagine breaking this 0.25 mm=250 μm film into 250 μm diameter droplets distributed uniformly-randomly in a 250 m thick cloud. This cloud has the same precipitable-water as the earlier hypothesized cloud, but in much larger droplets. In the process of scattering infrared light, the droplets will have roughly the same attenuation as the 0.25 mm film. Smaller droplets, such as those occuring in clouds, should have transmission between the two curves, both of which are negligible.
The change in direction of infrared photons by scattering affords opportunities for more scattering and hence even more attenuation.
Because of water's and ice's positive k, scattering by droplets absorbs infrared radiation, making water and ice clouds effective blackbodies for thermal radiation.
In Atmospheric radiation near the surface of the ground: A summary for engineers [52], R. Bliss simply treats clouds as infrared blackbody radiators.
Additional support is found in "Analysis of Visible and Infrared Cirrus Cloud Optical Properties Using High Spectral Remote Sensing,"[54]:
IR Scattering from Mie Model
The infrared scattering cross-section for molecules is much smaller than the absorption cross-section; and extinction in the IR is dominated by absorption such that scattering can be neglected. However, ice crystals and water droplets found in clouds are of similar magnitude or greater in size than wavelengths associated with IR radiation. Although extinction by absorption continues to dominate, scattering of upwelling terrestrial and atmospheric emission from below the cloud will provide a small contribution to the downwelling measured radiance...
Copyright © 2010 Aubrey Jaffer
|
I am a guest and not a member of the MIT Computer Science and Artificial Intelligence Laboratory.
My actions and comments do not reflect in any way on MIT. | ||
| Radiative Cooling in Hot Humid Climates | ||
| agj @ alum.mit.edu | Go Figure! | |