Research
I develop new theories and algorithms to improve learning from high-dimensional data. The "curse of dimensionality" tells us that such learning is generally intractable. However, various simplifying structures in practical problems exist and could be exploited in order to render learning in high dimensions tractable. My research focuses on revealing the hidden simplifying structures in high-dimensional problems using transformations, and is motivated by the two facts:
- Data Transforms. Parsimonious structures (e.g., sparsity, low-rank, etc.) are prevalent in high-dimensional
data. However, in many interesting applications, such structures reveal themselves only after appropriate transformations on the data.
For example, an urban image often forms a low-rank matrix, but only after the image is rectified.
In the illustrartive example, rank-two approximation (sum of two rank-one matrices) of an image by nonrectified (top)
and rectified (bottom) forms are shown. Here tau is a perspective transform. Notice that rank-two approximation has a better fidelity (sharper image in the right) when the effect of perspective is removed, compared to the one with perspective effect. I have this idea for segmentation and 3D reconstruction of http://people.csail.mit.edu/hmobahi/pubs/urban2011.pdf. Using similar concept but a different transformation, I have also used this idea for segmentation of natural images (a fundamental problem in computer vision), which led to state-of-the-art performance on benchmark data. Most recently, I have used similar ideas for image set representation.

- Objective Function Transforms.
In most hierarchical and cascaded models such as deep networks, the optimization problem associated with learning is often nonconvex,
which is generally intractable in high dimensions. However, applying proper transformations to the objective function
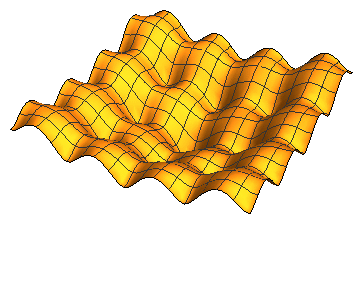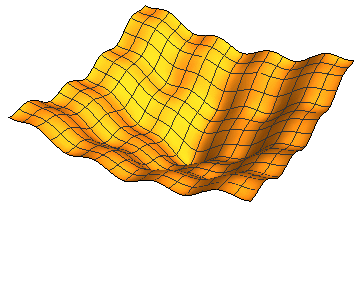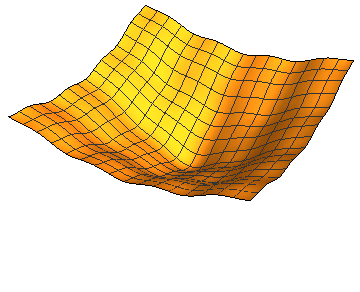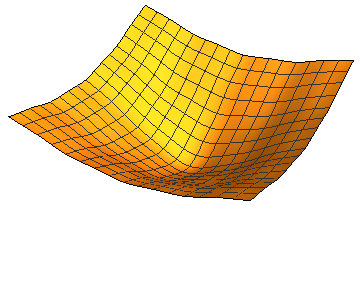
may facilitate optimization. For example, the following figure evolves a complex cost function by the diffusion equation to eventually create a unimodal function. My research on optimization makes extensive use of the diffusion equation for simplifying optimization. I have developed theories justifying diffusion for optimization and efficient algorithms to compute the diffused cost function in closed form and with performance guarantees. I have used the resulted algorithms in tasks involving visual alignment and matching. Currently I am investigating the benefits of this method in training recurrent neural networks where preliminary results show significant promise. These networks are very good in learning high dimensional sequential patterns, but the networks are known to be challenging to train compared to feedforward networks such as CNNs.
Using these transformations, my research expands the range of applications for which learning in high dimensions can be achieved efficiently. My entry point to analysis of high-dimensional learning was computer vision, but my recent research direction covers deep and fundamental aspects of such learning regime. The resulted theories and algorithms are likely to have benefit application domains involving learning from high-dimensional data such as robotics, NLP, data mining, etc. I am very excited to explore these avenues via collaboration.