Motivation
Color Space Dimension Reduction
explores methods of dimension reduction, focusing on space-filling
curves. For the purpose of presenting colors for selection, the
space-filling curve attributed to Hilbert seems to perform better than
the curve due to Peano. Can that difference be quantified?
The goal of dimension reduction is to find a mapping from a
higher-dimensional space to a lower-dimensional space where points
which are close in the higher-dimensional space map to points which
are close in the other space.
Apparatus
- 2009-06-10 Development version of SCM 5e5
- 2009-06-10 Development version of SLIB 3b1
- Scheme program closeness.scm
- the "convert" program, part of ImageMagick-6.3.2
Procedure
-
scm -l closeness.scm
- Graphs are written in the working directory:
- "Z-curve-r.png"
- Graph of Euclidean-distance /
scalar-distance versus the scalar-distance between two points
for the Z-curve in 2, 3, 4, and 6 dimensions.
- "Z-curve-l.png"
- Graph of the logarithm of
Euclidean-distance versus the logarithm of the scalar-distance
between two points for the Z-curve in 2, 3, 4, and 6 dimensions.
- "Peano-r.png"
- Graph of Euclidean-distance /
scalar-distance versus the scalar-distance between two points for
the Peano space-filling curve in 2, 3, 4, and 6 dimensions.
- "Peano-l.png"
- Graph of the logarithm of
Euclidean-distance versus the logarithm of the scalar-distance
between two points for the Peano space-filling curve in 2, 3, 4, and
6 dimensions.
- "Hilbert-r.png"
- Graph of Euclidean-distance /
scalar-distance versus the scalar-distance between two points for
the Hilbert space-filling curve in 2, 3, 4, and 6 dimensions.
- "Hilbert-l.png"
- Graph of the logarithm of
Euclidean-distance versus the logarithm of the scalar-distance
between two points for the Hilbert space-filling curve in 2, 3, 4,
and 6 dimensions.
Method
- The closeness.scm program fills an
array with the multidimensional coordinates corresponding to 4096
(or 729 for Peano curves) successive integers.
- For a given dimension it then computes, for each scalar-distance
from 1 to 15, the average ratio of Euclidean-distance to the
scalar-distance for all pairs of points having that scalar
separation.
- The resulting graphs are written to graphic files:
- "Z-curve-r.png"
- "Peano-r.png"
- "Hilbert-r.png"
- For a given dimension it then computes, for each scalar-distance
from 1 to 100, the logarithm of the average Euclidean-distance for
all pairs of points having that scalar separation.
- The resulting graphs are written to graphic files:
- "Z-curve-l.png"
- "Peano-l.png"
- "Hilbert-l.png"
Measurements
Analysis
 The Z-curve has
the widest spread and is particularly poor in 2-dimensions (the top
plot). Worse still is that most unit length scalar edges map to
coordinates which are more than one unit separated. Thus the average
displacement for unit edges averages above 1.6 for 2-dimensions and
above 1.35 for the other ranks.
The Z-curve has
the widest spread and is particularly poor in 2-dimensions (the top
plot). Worse still is that most unit length scalar edges map to
coordinates which are more than one unit separated. Thus the average
displacement for unit edges averages above 1.6 for 2-dimensions and
above 1.35 for the other ranks.
The ratios for all three functions quickly approach their low,
asymptotic values as the rank is increased. For the Peano and Hilbert
curves the traces for ranks 6 and 9 are coincident.
The space-filling curve attributed to
Peano maps scalar unit lengths to unit Euclidean lengths, giving
optimal behavior for the shortest length. In fact all horizontal
segments are exactly unit length. The vertical segments run 2 and 5
units; raising the averages in that range.
 The space-filling curve attributed to
Hilbert edges out the Peano curve to have the best performance of
those measured.
Color-Space Dimension
Reduction also finds the Hilbert curve (slightly) better
than Peano's.
And [Bongki 2001]
rates it best as well.
The space-filling curve attributed to
Hilbert edges out the Peano curve to have the best performance of
those measured.
Color-Space Dimension
Reduction also finds the Hilbert curve (slightly) better
than Peano's.
And [Bongki 2001]
rates it best as well.
Logarithmic Measurements
Plotting the (logarithm of) average Euclidean-distance versus the
(logarithm of) scalar-distance out to longer distances seems to
indicate that the roughness of the high rank curves does not become
smooth asymptotically.
Copyright © 2005, 2009 Aubrey Jaffer
I am a guest and not a member of the MIT Computer Science and Artificial Intelligence Laboratory.
My actions and comments do not reflect in any way on
MIT.
|
| | Computer Natural Science
|
| agj @ alum.mit.edu
| Go Figure!
|
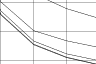




 The Z-curve has
the widest spread and is particularly poor in 2-dimensions (the top
plot). Worse still is that most unit length scalar edges map to
coordinates which are more than one unit separated. Thus the average
displacement for unit edges averages above 1.6 for 2-dimensions and
above 1.35 for the other ranks.
The Z-curve has
the widest spread and is particularly poor in 2-dimensions (the top
plot). Worse still is that most unit length scalar edges map to
coordinates which are more than one unit separated. Thus the average
displacement for unit edges averages above 1.6 for 2-dimensions and
above 1.35 for the other ranks.

 The space-filling curve attributed to
Hilbert edges out the Peano curve to have the best performance of
those measured.
Color-Space Dimension
Reduction also finds the Hilbert curve (slightly) better
than Peano's.
And [Bongki 2001]
rates it best as well.
The space-filling curve attributed to
Hilbert edges out the Peano curve to have the best performance of
those measured.
Color-Space Dimension
Reduction also finds the Hilbert curve (slightly) better
than Peano's.
And [Bongki 2001]
rates it best as well.


