http://people.csail.mit.edu/jaffer/Geometry/PSFC
	Peano Space-Filling Curves

Space-filling curves serve as a counterexample to less-than-rigorous notions of dimension. In addition to their mathematical importance, space-filling curves have applications to dimension reduction, mathematical programming [Butz 1968], multi-dimensional database indexing [Lawder 2000], and radio-frequency electronics [Zhu 2003].

The space-filling constructions are usually designed to map between the real unit line segment and the unit n-cube. My interest is to expand their range to the entirety of n-space.

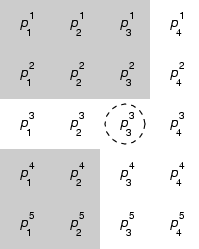
The Algorithm

Digit i of row j, p_jⁱ, is replaced by 2-p_jⁱ if the integer sum of:

• all the digits in columns left of column j which are not in row i and
• the digits in column j above row i

Notice that the parity (zero vs. nonzero) of digit p_jⁱ remains unchanged when it is replaced by 2-p_jⁱ. Thus the order of processing digits is arbitrary. This peano-flip! operation is its own inverse.

A naive implementation would take time O(mn²) for the complete table. By scanning down each column from left to right while calculating the total parity and the parity for the portion of each row already visited, this can be reduced to O(mn).

Here is the simplest case. Groups of flipped digits are underlined.

scalar	0	1	2	3	4	5	6	7	8
digits	0 0	0 1	0 2	1 0	1 1	1 2	2 0	2 1	2 2
flipped	0 0	0 1	0 2	1 2	1 1	1 0	2 0	2 1	2 2

So within a 3*3 cell an odd higher digit flips the lower digit, creating the signature S curve.

scalar	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27
digits	0 0 1 0	0 0 1 1	0 0 1 2	0 1 1 0	0 1 1 1	0 1 1 2	0 2 1 0	0 2 1 1	0 2 1 2	0 0 2 0	0 0 2 1	0 0 2 2	0 1 2 0	0 1 2 1	0 1 2 2	0 2 2 0	0 2 2 1	0 2 2 2	1 0 0 0
flipped	0 2 1 0	0 2 1 1	0 2 1 2	0 1 1 2	0 1 1 1	0 1 1 0	0 0 1 0	0 0 1 1	0 0 1 2	0 0 2 0	0 0 2 1	0 0 2 2	0 1 2 2	0 1 2 1	0 1 2 0	0 2 2 0	0 2 2 1	0 2 2 2	1 0 2 2

From 0 to 8 we have seen digits increment or decrement only by 1. From 8 to 9, 17 to 18, and 26 to 27 the low order digit jumps from 2 to 0 while carrying into the digit to its left.

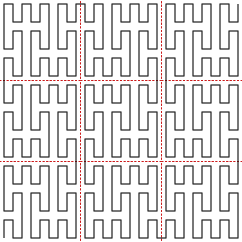
The Curve

The horizontal segments in the curve at right are all the same length. Vertical segments, however, are two and five times the horizontal length.

Long straight segments degrade the closeness-preserving properties important to many applications. Where a linear distance of 5 units may map to an n-space distance of 5 in this curve, in a wigglier curve it would always map to a shorter distance.

This suggests that a figure-of-merit for space-filling curves would be to sum, for every pair of m-digit points in n-space, the ratio of the euclidean distance to its corresponding linear distance. The Performance of Space-Filling Curves for Dimension Reduction reports the results of such measurements.

Wigglier

Generalizing this to higher ranks is not straightforward. Each 3-dimensional cell connects along one of three diagonals of the cube.

Centering

Also useful would be a space-filling curve covering all integer coordinates, Zⁿ. Although each 3^mn point curve is symmetrical around its center, the coordinates calculated by the algorithm given above are nonnegative. Although the conversion from the digit table to n-space coordinates could subtract one from each digit; because the number of digits is autoscaled, discontinuities result at 3^mn boundaries.

More fundamental is that, if all of n-space is to be covered by a double-ended self-similar curve, then negative linear numbers must paint half of it. Thus the positive half of linear numbers in the range -3^mn/2 to 3^mn/2 must paint a shape other than a square. Fortunately, they form what could be described as a rectilinear spiral:

The algorithm to convert from an integer scalar to n centered Peano coordinates is:

• Find the smallest m such that 9^mn/2 is greater or equal to absolute-value of scalar;
• Convert scalar + 9^mn/2 into a ternary digit array;
• peano-flip! the ternay digit array;
• extract each coordinate from its array row; offsetting it by -9^m/2.

The algorithm to convert from n centered Peano coordinates to an integer scalar is:

• Find the smallest m such that 9^m/2 is greater or equal to the absolute-value of each the input coordinate.
• Convert the coordinates offset by +9^m/2 into a ternary digit array;
• peano-flip! the ternay digit array;
• extract the scalar from the array; offsetting it by -9^mn/2.

The divisions all round toward zero. The base of the exponents is 9 rather than 3 because, although the center square of the 3^m scale cube has the same orientation as the corner squares, it is traversed in the reverse direction.

Praxis

Function: natural->peano-coordinates scalar rank

Returns a list of rank nonnegative integer coordinates corresponding to exact nonnegative integer scalar. The lists returned by natural->peano-coordinates for scalar arguments 0 and 1 will differ in the first element.

Function: peano-coordinates->natural coords

Returns an exact nonnegative integer corresponding to coords, a list of nonnegative integer coordinates.

Function: integer->peano-coordinates scalar rank

Returns a list of rank integer coordinates corresponding to exact integer scalar. The lists returned by integer->peano-coordinates for scalar arguments 0 and 1 will differ in the first element.

Function: peano-coordinates->integer coords

Returns an exact integer corresponding to coords, a list of integer coordinates.

Further Work

• Develop a "wigglier" variant of the Peano curve.

  The Peano curve described here does not have the isotropy property called for by Multidimensional Space-Filling Curves:

  the lengths of axis-aligned projections of the space-filling curve should be equal.

  The Peano curve reflects cells in order to make them contiguous, but does not perform the rotation causing such vexation in Recursive Formulation of Multidimensional Space-Filling Functions

  It should be possible to rotate those cells currently subject to an odd number of reflections. That would rotate 4 of the 9 subcells of each cell.

• Write comparison functions for Peano fixed-point coordinates.

• Write comparison functions for Peano floating-point coordinates.

• Use these functions to extend the WB B-trees to multidimensional indexes a la [Lawder 2000].