6.440 Essential Coding Theory
Fall 2011, TR1-2:30, 32-144, 3-0-9 H Level Grad Credit
Instructor: Dana Moshkovitz
·
Subject requirements and syllabus
Lectures:
|
Date |
Title |
Reading |
|
9/8/11 |
Hamming’s
Paper: Hamming distance, Hamming Code |
·
Historic background (Shannon and Hamming) |
|
9/13/11 |
Shannon’s Paper:
Shannon entropy, Shannon’s Noisy Coding Theorem |
|
|
9/15/11 |
Non-explicit Constructions:
Gilbert, Varshamov |
|
|
9/20/11 |
Lower Bounds:
Singleton, Hamming, Plotkin and Elias-Bassalygo Bounds, Johnson Bound |
|
|
9/22/11 |
Algebraic Codes:
Reed-Solomon, Reed-Muller, Hadamard, BCH Codes |
·
Madhu’s notes (&
algebra review) |
|
9/27/11 |
Concatenation:
Wozencraft Ensemble, Justensen
Codes, concatenation with hitters |
|
|
9/29/11 |
Algebraic-Geometry Codes: History
starting Goppa, elementary example improving
Reed-Muller, statement of Garcia-Stichtenoth |
|
|
10/4/11 |
Linear Programming Bound:
Delsarte’s approach, MacWilliams
Identity, Alon’s proof of a comparable bound. |
|
|
10/6/11 |
Decoding Reed-Solomon and Concatenated
Codes: Berlekamp-Welch
with variants, generalizations, applications. |
|
|
10/11/11 |
Columbus Day Weekend |
|
|
10/13/11 |
List Decoding:
proof of Johnson bound, rate vs. radius |
|
|
10/18/11 |
List Decoding of Reed-Solomon:
Sudan and Guruswami-Sudan algorithms |
|
|
10/20/11 |
Capacity-achieving List Decoding: Parvaresh-Vardy,
Guruswami-Rudra |
|
|
10/25/11 |
LDPC Codes:
Gallager, Tanner, Sipser-Spielman |
|
|
10/27/11 |
Decoding LDPC Codes:
Sipser-Spielman |
·
Venkat’s survey:
LDPC codes can achieve channel capacity? |
|
11/1/11 |
No lecture |
|
|
11/3/11 |
Linear-Time Encodable
and Decodable Codes: Spielman |
|
|
11/8/11 |
Expander Codes:
Alon-Brooks-Naor-Naor-Roth (ABNNR), Alon-Edmonds-Luby, Guruswami-Indyk |
|
|
11/10/11 |
Locally Decodable Codes:
Reed-Muller, Yekhanin’s construction (simpler
presentation) |
|
|
11/15/11 |
Locally Decodable Codes Lower Bounds:
Katz-Trevisan |
|
|
11/17/11 |
Locally Testable Codes:
Blum-Luby-Rubinfeld
linearity testing, low degree testing |
|
|
11/22/11 |
Codes in Crypto & Communication
Complexity: hard-core predicates, secret sharing,
communication complexity of equality testing |
|
|
11/29/11 |
Multiplicity Codes (Madhu):
Kopparty-Saraf-Yekhanin |
·
Kopparty-Saraf-Yekhanin paper |
|
12/1/11 |
Codes and Extractors (Madhu) |
|
|
12/6/11 |
Pesudorandom
Generators From Codes: Sudan-Vadhan-Trevisan, Nisan-Wigderson |
|
|
12/8/11 |
6.440 Projects Presentation I |
|
|
12/13/11 |
6.440 Projects Presentation II |
Problem Sets:
1.
Problem Set 1, due September 27, 2011.
2.
Problem Set 2, due October 18, 2011. / A version without hints.
3.
Problem Set 3, due November 22, 2011.
Frequently Asked Questions:
What
are Error Correcting Codes?
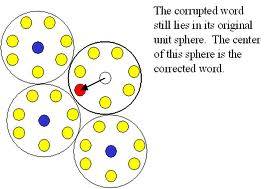
Error correcting codes are redundant ways to represent information, so it becomes resilient to bounded amount of error.
Formally, a (binary) encoding is a function E:{0,1}k->{0,1}n that takes k bits of information and encodes them with n bits of redundant information, such that for every two different strings of information x,y, the strings E(x) and E(y) agree (i.e., E(x)i=E(y)i) on not much more than n/2 coordinates.
Hence, even if nearly quarter of the n symbols in the encoding get corrupted, we can still figure out the information!
What
does the Subject Cover?
The subject covers constructions of codes, bounds (e.g., how large should n be as a function of k? What’s the maximal amount of error that can be tolerated?), algorithms for encoding and decoding, and applications of error correcting codes to theoretical computer science.
Why do
Theoretical Computer Scientists Care About Codes?
Error correcting codes are used frequently in complexity, cryptography and algorithms, and are in the heart of some of the central results of theoretical computer science, like:
· Communication complexity: how two players, one with a string x in {0,1}k, and one with a string y in {0,1}k, can probabilistically discover whether x=y by exchanging just one bit!
· Average case vs worst case: how to reduce certain worst case problems, like the permanent, to average case problems.
· Hardness vs Randomness tradeoffs: how to use hard functions to construct pseudorandom generators.
· Hard-core predicates: how to find a Boolean predicate H(x) that is easy to compute given x, but hard to compute from the image of a one-way function f(x).
· The Probabilistically Checkable Proofs (PCP) Theorem: how to convert any math proof to a format that allows probabilistic checking by reading only a constant number of bits.
What are the prerequisites for the subject?
Basic math (discrete math, linear algebra, probability),
algorithms (6.046 or equivalent),
and complexity (6.045 or 6.840 or equivalent).
What
are the subject’s requirements?
Students are asked to solve 4 psets and do a project.
More information?
The best way to know what the subject is going to be like is to take a look at
previous offerings of the subject,
by Madhu Sudan: