We consider the dictionary problem in external memory and improve the update
time of the well-known buffer tree by roughly a logarithmic factor. For any
λ ≥ max{lg lg n,log M∕B(n∕B)}, we can support updates in time O(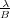 ) and queries in
time O(log λn). We also present a lower bound in the cell-probe model showing that
our data structure is optimal. ) and queries in
time O(log λn). We also present a lower bound in the cell-probe model showing that
our data structure is optimal.
In the RAM, hash tables have been use to solve the dictionary problem
faster than binary search for more than half a century. By contrast, our data
structure is the first to beat the comparison barrier in external memory. Ours is
also the first data structure to depart convincingly from the indivisibility
paradigm.
|
Timothy M. Chan,
Kasper Larsen,
and Mihai Pătraşcu
27th ACM Symposium on Computational Geometry ( SoCG 2011).
Full version: arXiv:1011.5200.
Invited to special issue of Computational Geometry: Theory and Applications (CGTA); declined.
We present a number of new results on one of the most extensively studied topics
in computational geometry, orthogonal range searching. All our results are in the
standard word RAM model:
- We present two data structures for 2-d orthogonal range emptiness. The
first achieves O(nlg lg n) space and O(lg lg n) query time, assuming that
the n given points are in rank space. This improves the previous results
by Alstrup, Brodal, and Rauhe (FOCS’00), with O(nlg εn) space and
O(lg lg n) query time, or with O(nlg lg n) space and O(lg 2 lg n) query
time. Our second data structure uses O(n) space and answers queries
in O(lg εn) time. The best previous O(n)-space data structure, due to
Nekrich (WADS’07), answers queries in O(lg n∕lg lg n) time.
- We give a data structure for 3-d orthogonal range reporting with
O(nlg 1+εn) space and O(lg lg n + k) query time for points in rank space,
for any constant ε > 0. This improves the previous results by Afshani
(ESA’08), Karpinski and Nekrich (COCOON’09), and Chan (SODA’11),
with O(nlg 3n) space and O(lg lg n + k) query time, or with O(nlg 1+εn)
space and O(lg 2 lg n + k) query time. Consequently, we obtain improved
upper bounds for orthogonal range reporting in all constant dimensions
above 3.
Our approach also leads to a new data structure for 2-d orthogonal range
minimum queries with O(nlg εn) space and O(lg lg n) query time for points
in rank space.
- We give a randomized algorithm for 4-d offline dominance range
reporting/emptiness with running time O(nlog n) plus the output size. This
resolves two open problems (both appeared in Preparata and Shamos’ seminal
book):
- given a set of n axis-aligned rectangles in the plane, we can report
all k enclosure pairs (i.e., pairs (r1,r2) where rectangle r1 completely
encloses rectangle r2) in O(nlg n + k) expected time;
- given a set of n points in 4-d, we can find all maximal points (points
not dominated by any other points) in O(nlg n) expected time.
The most recent previous development on (a) was reported back in SoCG’95 by
Gupta, Janardan, Smid, and Dasgupta, whose main result was an
O([nlg n + k]lg lg n) algorithm. The best previous result on (b) was an
O(nlg nlg lg n) algorithm due to Gabow, Bentley, and Tarjan—from STOC’84!
As a consequence, we also obtain the current-record time bound for the maxima
problem in all constant dimensions above 4.
|
Mihai Pătraşcu
and Mikkel Thorup
43rd ACM Symposium on Theory of Computing ( STOC 2011).
In submission to J. ACM. Full version:: arXiv:1011.5200.
Randomized algorithms are often enjoyed for their simplicity, but the hash
functions used to yield the desired theoretical guarantees are often neither simple nor
practical. Here we show that the simplest possible tabulation hashing provides
unexpectedly strong guarantees.
The scheme itself dates back to Carter and Wegman (STOC’77). Keys are viewed
as consisting of c characters. We initialize c tables T1,…,Tc mapping characters to
random hash codes. A key x = (x1,…,xq) is hashed to T1[x1] ⊕ ⊕Tc[xc], where ⊕
denotes xor. ⊕Tc[xc], where ⊕
denotes xor.
While this scheme is not even 4-independent, we show that it provides many of
the guarantees that are normally obtained via higher independence, e.g.,
Chernoff-type concentration, min-wise hashing for estimating set intersection, and
cuckoo hashing.
|
We present a new threshold phenomenon in data structure lower bounds where
slightly reduced update times lead to exploding query times. Consider incremental
connectivity, letting tu be the time to insert an edge and tq be the query time. For
tu = Ω(tq), the problem is equivalent to the well-understood union–find problem:
InsertEdge(s,t) can be implemented by Union(Find(s),Find(t)). This gives
worst-case time tu = tq = O(lg n∕lg lg n) and amortized tu = tq = O(α(n)).
By contrast, we show that if tu = o(lg n∕lg lg n), the query time explodes to
tq ≥ n1-o(1). In other words, if the data structure doesn’t have time to find the roots
of each disjoint set (tree) during edge insertion, there is no effective way to organize
the information!
For amortized complexity, we demonstrate a new inverse-Ackermann type
trade-off in the regime tu = o(tq).
A similar lower bound is given for fully dynamic connectivity, where an update
time of o(lg n) forces the query time to be n1-o(1). This lower bound allows for
amortization and Las Vegas randomization, and comes close to the known
O(lg n ⋅ (lg lg n)O(1)) upper bound.
|
Mihai Pătraşcu
and Liam Roditty
51st IEEE Symposium on Foundations of Computer Science ( FOCS 2010).
We give the first improvement to the space/approximation trade-off of distance
oracles since the seminal result of Thorup and Zwick [STOC’01].
For unweighted graphs, our distance oracle has size O(n5∕3) = O(n1.66 )
and, when queried about vertices at distance d, returns a path of length
2d + 1. )
and, when queried about vertices at distance d, returns a path of length
2d + 1.
For weighted graphs with m = n2∕α edges, our distance oracle has size O(n2∕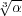 )
and returns a factor 2 approximation. )
and returns a factor 2 approximation.
Based on a widely believed conjecture about the hardness of set intersection
queries, we show that a 2-approximate distance oracle requires space 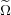 (n2∕ (n2∕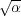 ).
For unweighted graphs, this implies a ).
For unweighted graphs, this implies a 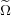 (n1.5) space lower bound to achieve
approximation 2d + 1. (n1.5) space lower bound to achieve
approximation 2d + 1.
|
Mihai Pătraşcu
and Mikkel Thorup
37th International Colloquium on Automata, Languages and Programming ( ICALP 2010).
We show that linear probing requires 5-independent hash functions for expected
constant-time performance, matching an upper bound of [Pagh et al. STOC’07]. For
(1 + ε)-approximate minwise independence, we show that Ω(lg 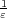 )-independent hash
functions are required, matching an upper bound of [Indyk, SODA’99]. We also show
that the multiply-shift scheme of Dietzfelbinger, most commonly used in practice,
fails badly in both applications. )-independent hash
functions are required, matching an upper bound of [Indyk, SODA’99]. We also show
that the multiply-shift scheme of Dietzfelbinger, most commonly used in practice,
fails badly in both applications.
|
Mihai Pătraşcu
42nd ACM Symposium on Theory of Computing ( STOC 2010).
We consider a number of dynamic problems with no known poly-logarithmic
upper bounds, and show that they require nΩ(1) time per operation, unless 3SUM has
strongly subquadratic algorithms. Our result is modular:
1. We describe a carefully-chosen dynamic version of set disjointness (the
multiphase problem), and conjecture that it requires nΩ(1) time per operation. All our
lower bounds follow by easy reduction.
2. We reduce 3SUM to the multiphase problem. Ours is the first nonalgebraic
reduction from 3SUM, and allows 3SUM-hardness results for combinatorial
problems. For instance, it implies hardness of reporting all triangles in a
graph.
3. It is possible that an unconditional lower bound for the multiphase problem
can be established via a number-on-forehead communication game.
|
We describe a simple, but powerful local encoding technique, implying two
surprising results:
1. We show how to represent a vector of n values from Σ using ⌈nlog 2Σ⌉ bits,
such that reading or writing any entry takes O(1) time. This demonstrates, for
instance, an “equivalence” between decimal and binary computers, and has been a
central toy problem in the field of succinct data structures. Previous solutions
required space of nlog 2Σ + n∕lg O(1)n bits for constant access.
2. Given a stream of n bits arriving online (for any n, not known in advance), we
can output a prefix-free encoding that uses n + log 2n + O(lg lg n) bits. The encoding
and decoding algorithms only require O(lg n) bits of memory, and run in constant
time per word. This result is interesting in cryptographic applications, as prefix-free
codes are the simplest counter-measure to extensions attacks on hash functions,
message authentication codes and pseudorandom functions. Our result refutes a
conjecture of [Maurer, Sjödin 2005] on the hardness of online prefix-free
encodings.
|
Mihai Pătraşcu
and Dan Strătilă
In preparation. Talk in 20th International Symposium of Mathematical Programming (ISMP 2009).
We consider the classical lot-sizing problem, introduced by Manne (1958), and
Wagner and Whitin (1958). Since its introduction, much research has investigated
the running time of this problem. Federgruen and Tzur (1991), Wagelmans et al.
(1992), and Aggarwal and Park (1993) independently obtained O(nlg n) algorithms.
Recently, Levi et al. (2006) developed a primal-dual algorithm. Building on the
work of Levi et al., we obtain a faster algorithm with a running time of
O(nlg lg n).
|
Mihai Pătraşcu
and Emanuele Viola
21st ACM/SIAM Symposium on Discrete Algorithms ( SODA 2010).
The partial sums problem in succinct data structures asks to preprocess an array
A[1..n] of bits into a data structure using as close to n bits as possible, and
answer queries of the form rank(k) = ∑
i=1kA[i]. The problem has been
intensely studied, and features as a subroutine in a number of succinct data
structures.
We show that, if we answer rank queries by probing t cells of w bits, then the
space of the data structure must be at least n + n∕wO(t) bits. This redundancy/probe
trade-off is essentially optimal: Patrascu [FOCS’08] showed how to achieve
n + n∕(w∕t)Ω(t) bits. We also extend our lower bound to the closely related select
queries, and to the case of sparse arrays.
|
Mihai Pătraşcu
and Ryan Williams
21st ACM/SIAM Symposium on Discrete Algorithms ( SODA 2010).
We describe reductions from the problem of determining the satisfiability of
Boolean CNF formulas (CNF-SAT) to several natural algorithmic problems. We show
that attaining any of the following bounds would improve the state of the art in
algorithms for SAT:
- an O(nk-ε) algorithm for k-Dominating Set, for any k ≥ 3,
- a (computationally efficient) protocol for 3-party set disjointness with
o(m) bits of communication,
- an no(d) algorithm for d-SUM,
- an O(n2-ε) algorithm for 2-SAT with m = n1+o(1) clauses, where two
clauses may have unrestricted length, and
- an O((n+m)k-ε) algorithm for HornSat with k unrestricted length clauses.
One may interpret our reductions as new attacks on the complexity of SAT, or sharp
lower bounds conditional on exponential hardness of SAT.
|
Timothy M. Chan
and Mihai Pătraşcu
21st ACM/SIAM Symposium on Discrete Algorithms ( SODA 2010).
We give an O(n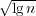 )-time algorithm for counting the number of inversions in a
permutation on n elements. This improves a long-standing previous bound of
O(nlg n∕lg lg n) that followed from Dietz’s data structure [WADS’89], and answers a
question of Andersson and Petersson [SODA’95]. As Dietz’s result is known to be
optimal for the related dynamic rank problem, our result demonstrates a significant
improvement in the offline setting. )-time algorithm for counting the number of inversions in a
permutation on n elements. This improves a long-standing previous bound of
O(nlg n∕lg lg n) that followed from Dietz’s data structure [WADS’89], and answers a
question of Andersson and Petersson [SODA’95]. As Dietz’s result is known to be
optimal for the related dynamic rank problem, our result demonstrates a significant
improvement in the offline setting.
Our new technique is quite simple: we perform a “vertical partitioning” of a trie
(akin to van Emde Boas trees), and use ideas from external memory. However, the
technique finds numerous applications: for example, we obtain
- in d dimensions, an algorithm to answer n offline orthogonal range
counting queries in time O(nlg d-2+1∕dn);
- an improved construction time for online data structures for orthogonal
range counting;
- an improved update time for the partial sums problem;
- faster Word RAM algorithms for finding the maximum depth in an
arrangement of axis-aligned rectangles, and for the slope selection
problem.
As a bonus, we also give a simple (1 + ε)-approximation algorithm for counting
inversions that runs in linear time, improving the previous O(nlg lg n) bound by
Andersson and Petersson.
|
We prove that any sketching protocol for edit distance achieving a constant
approximation requires nearly logarithmic (in the strings’ length) communication
complexity. This is an exponential improvement over the previous, doubly-logarithmic,
lower bound of [Andoni-Krauthgamer, FOCS’07]. Our lower bound also applies to the
Ulam distance (edit distance over non-repetitive strings). In this special case, it is
polynomially related to the recent upper bound of [Andoni-Indyk-Krauthgamer,
SODA’09].
From a technical perspective, we prove a direct-sum theorem for sketching
product metrics that is of independent interest. We show that, for any metric X
that requires sketch size which is a sufficiently large constant, sketching the
max-product metric ℓ∞d(X) requires Ω(d) bits. The conclusion, in fact, also holds
for arbitrary two-way communication. The proof uses a novel technique
for information complexity based on Poincaré inequalities and suggests an
intimate connection between non-embeddability, sketching and communication
complexity.
|
We present a novel connection between binary search trees (BSTs) and points in
the plane satisfying a simple property. Using this correspondence, we achieve the
following results:
- A surprisingly clean restatement in geometric terms of many results and
conjectures relating to BSTs and dynamic optimality.
- A new lower bound for searching in the BST model, which subsumes the
previous two known bounds of Wilber [FOCS’86].
- The first proposal for dynamic optimality not based on splay trees. A
natural greedy but offline algorithm was presented by Lucas [1988], and
independently by Munro [2000], and was conjectured to be an (additive)
approximation of the best binary search tree. We show that there exists
an equal-cost online algorithm, transforming the conjecture of Lucas
and Munro into the conjecture that the greedy algorithm is dynamically
optimal.
|
Mihai Pătraşcu
SIAM Journal on Computing ( SICOMP), vol. 40(3), 2011. Special issue.
49th IEEE Symposium on Foundations of Computer Science ( FOCS 2008).
Also available as: arXiv:1010.3783.
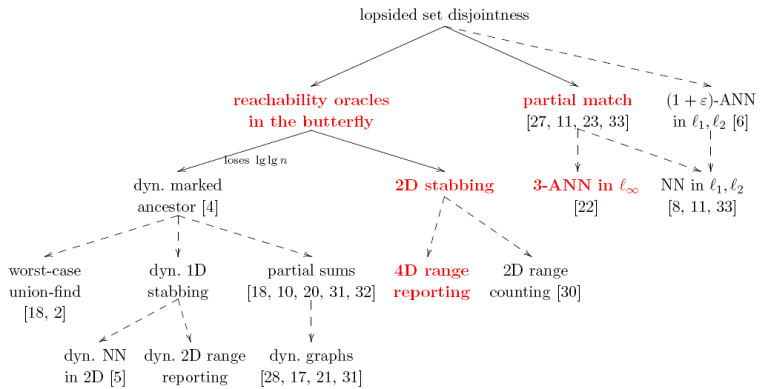
We show that a large fraction of the data-structure lower bounds known today in
fact follow by reduction from the communication complexity of lopsided
(asymmetric) set disjointness! This includes lower bounds for:
- high-dimensional problems, where the goal is to show large space lower
bounds.
- constant-dimensional geometric problems, where the goal is to bound the
query time for space O(npolylogn).
- dynamic problems, where we are looking for a trade-off between query
and update time. (In this case, our bounds are slightly weaker than the
originals, losing a lg lg n factor.)
Our reductions also imply the following new results:
- an Ω(lg n∕lg lg n) bound for 4-dimensional range reporting, given
space O(npolylogn). This is very timely, since a recent result
[Nekrich, SoCG’07] solved 3D reporting in near-constant time, raising the
prospect that higher dimensions could also be easy.
- a tight space lower bound for the partial match problem, for constant
query time.
- the first lower bound for reachability oracles.
In the process, we prove optimal randomized lower bounds for lopsided set
disjointness.
|
Mihai Pătraşcu
49th IEEE Symposium on Foundations of Computer Science ( FOCS 2008).
Best Student Paper (the Machtey Award)
We can represent an array of n values from {0,1,2} using 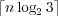 bits
(arithmetic coding), but then we cannot retrieve a single element efficiently. Instead,
we can encode every block of t elements using bits
(arithmetic coding), but then we cannot retrieve a single element efficiently. Instead,
we can encode every block of t elements using 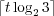 bits, and bound the
retrieval time by t. This gives a linear trade-off between the redundancy of the
representation and the query time. bits, and bound the
retrieval time by t. This gives a linear trade-off between the redundancy of the
representation and the query time.
In fact, this type of linear trade-off is ubiquitous in known succinct data
structures, and in data compression. The folk wisdom is that if we want to waste one
bit per block, the encoding is so constrained that it cannot help the query in any
way. Thus, the only thing a query can do is to read the entire block and unpack
it.
We break this limitation and show how to use recursion to improve redundancy. It
turns out that if a block is encoded with two (!) bits of redundancy, we can decode a
single element, and answer many other interesting queries, in time logarithmic in the
block size.
Our technique allows us to revisit classic problems in succinct data structures,
and give surprising new upper bounds. We also construct a locally-decodable version
of arithmetic coding.
|
Recent years have seen a significant increase in our understanding of
high-dimensional nearest neighbor search (NNS) for distances like the ℓ1 and ℓ2
norms. By contrast, our understanding of the ℓ∞ norm is now where it was (exactly)
10 years ago.
In FOCS’98, Indyk proved the following unorthodox result: there is a data
structure (in fact, a decision tree) of size O(nρ), for any ρ > 1, which achieves
approximation O(log ρ log d) for NNS in the d-dimensional ℓ∞ metric.
In this paper, we provide results that indicate that Indyk’s unconventional
bound might in fact be optimal. Specifically, we show a lower bound for the
asymmetric communication complexity of NNS under ℓ∞, which proves that this
space/approximation trade-off is optimal for decision trees and for data structures
with constant cell-probe complexity.
|
Dynamic connectivity is a well-studied problem, but so far the most
compelling progress has been confined to the edge-update model: maintain an
understanding of connectivity in an undirected graph, subject to edge insertions and
deletions. In this paper, we study two more challenging, yet equally fundamental
problems:
Subgraph connectivity asks to maintain an understanding of connectivity
under vertex updates: updates can turn vertices on and off, and queries refer to the
subgraph induced by on vertices. (For instance, this is closer to applications in
networks of routers, where node faults may occur.)
We describe a data structure supporting vertex updates in 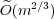 amortized time, where m denotes the number of edges in the graph. This greatly
improves over the previous result [Chan, STOC’02], which required fast matrix
multiplication and had an update time of O(m0.94). The new data structure is also
simpler.
amortized time, where m denotes the number of edges in the graph. This greatly
improves over the previous result [Chan, STOC’02], which required fast matrix
multiplication and had an update time of O(m0.94). The new data structure is also
simpler.
Geometric connectivity asks to maintain a dynamic set of n geometric objects,
and query connectivity in their intersection graph. (For instance, the intersection
graph of balls describes connectivity in a network of sensors with bounded
transmission radius.)
Previously, nontrivial fully dynamic results were known only for special cases like
axis-parallel line segments and rectangles. We provide similarly improved
update times, 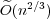 , for these special cases. Moreover, we show how
to obtain sublinear update bounds for virtually all families of geometric
objects which allow sublinear-time range queries. In particular, we obtain the
first sublinear update time for arbitrary 2D line segments: , for these special cases. Moreover, we show how
to obtain sublinear update bounds for virtually all families of geometric
objects which allow sublinear-time range queries. In particular, we obtain the
first sublinear update time for arbitrary 2D line segments: 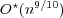 ;
for d-dimensional simplices: ;
for d-dimensional simplices: 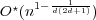 ; and for d-dimensional balls: ; and for d-dimensional balls:
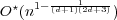 . .

|
We present the first sublinear-time algorithms for computing order statistics in
the Farey sequence and for the related problem of ranking. Our algorithms achieve a
running times of nearly O(n2∕3), which is a significant improvement over the previous
algorithms taking time O(n).
We also initiate the study of a more general problem: counting primitive lattice
points inside planar shapes. For rational polygons containing the origin, we
obtain a running time proportional to D6∕7, where D is the diameter of the
polygon.
|
|
|
Mihai Pătraşcu
and Mikkel Thorup
48th IEEE Symposium on Foundations of Computer Science ( FOCS 2007).
Understanding how a single edge deletion can affect the connectivity of a graph
amounts to finding the graph bridges. But when faced with d > 1 deletions, can we
establish as easily how the connectivity changes? When planning for an emergency,
we want to understand the structure of our network ahead of time, and respond
swiftly when an emergency actually happens.
We describe a linear-space representation of graphs which enables us to determine
how a batch of edge updates can impact the graph. Given a set of d edge updates, in
time O(dpolylogn) we can obtain the number of connected components,
the size of each component, and a fast oracle for answering connectivity
queries in the updated graph. The initial representation is polynomial-time
constructible.
|
It is well known that n integers in the range [1,nc] can be sorted in O(n) time in
the RAM model using radix sorting. More generally, integers in any range [1,U] can
be sorted in 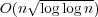 time. However, these algorithms use O(n) words of
extra memory. Is this necessary? time. However, these algorithms use O(n) words of
extra memory. Is this necessary?
We present a simple, stable, integer sorting algorithm for words of size O(log n),
which works in O(n) time and uses only O(1) words of extra memory on a RAM
model. This is the integer sorting case most useful in practice. We extend this result
with same bounds to the case when the keys are read-only, which is of theoretical
interest. Another interesting question is the case of arbitrary c. Here we present a
black-box transformation from any RAM sorting algorithm to a sorting
algorithm which uses only O(1) extra space and has the same running time.
This settles the complexity of in-place sorting in terms of the complexity of
sorting.
|
Mihai Pătraşcu
39th ACM Symposium on Theory of Computing ( STOC 2007).
Proving lower bounds for range queries has been an active topic of research since
the late 70s, but so far nearly all results have been limited to the (rather restrictive)
semigroup model. We consider one of the most basic range problem, orthogonal range
counting in two dimensions, and show almost optimal bounds in the group model and
the (holy grail) cell-probe model.
Specifically, we show the following bounds, which were known in the semigroup
model, but are major improvements in the more general models:
- In the group and cell-probe models, a static data structure of size
nlg O(1)n requires Ω(lg n∕lg lg n) time per query. This is an exponential
improvement over previous bounds, and matches known upper bounds.
- In the group model, a dynamic data structure takes time
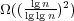 per operation. This is close to the O(lg 2n) upper bound, whereas the
previous lower bound was Ω(lg n).
per operation. This is close to the O(lg 2n) upper bound, whereas the
previous lower bound was Ω(lg n).
Proving such (static and dynamic) bounds in the group model has been regarded as
an important challenge at least since [Fredman, JACM 1982] and [Chazelle, FOCS
1986].
|
Timothy M. Chan
and Mihai Pătraşcu
39th ACM Symposium on Theory of Computing ( STOC 2007).
Journal version (submitted): arXiv:1010.1948.
The conference title was "Voronoi Diagrams in n•2O(√lglg n) Time"
We reexamine fundamental problems from computational geometry in the word
RAM model, where input coordinates are integers that fit in a machine word. We
develop a new algorithm for offline point location, a two-dimensional analog of
sorting where one needs to order points with respect to segments. This result implies,
for example, that the convex hull of n points in three dimensions can be constructed
in (randomized) time n ⋅ 2O(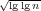 ). Similar bounds hold for numerous other
geometric problems, such as planar Voronoi diagrams, planar off-line nearest
neighbor search, line segment intersection, and triangulation of non-simple
polygons. ). Similar bounds hold for numerous other
geometric problems, such as planar Voronoi diagrams, planar off-line nearest
neighbor search, line segment intersection, and triangulation of non-simple
polygons.
In FOCS’06, we developed a data structure for online point location, which
implied a bound of O(n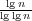 ) for three-dimensional convex hulls and the other
problems. Our current bounds are dramatically better, and a convincing
improvement over the classic O(nlg n) algorithms. As in the field of integer sorting,
the main challenge is to find ways to manipulate information, while avoiding the
online problem (in that case, predecessor search). ) for three-dimensional convex hulls and the other
problems. Our current bounds are dramatically better, and a convincing
improvement over the classic O(nlg n) algorithms. As in the field of integer sorting,
the main challenge is to find ways to manipulate information, while avoiding the
online problem (in that case, predecessor search).
|
Erik Demaine
and Mihai Pătraşcu
23rd ACM Symposium on Computational Geometry ( SoCG 2007).
The dynamic convex hull problem was recently solved in O(lg n) time per
operation, and this result is best possible in models of computation with bounded
branching (e.g., algebraic computation trees). From a data structures point of view,
however, such models are considered unrealistic because they hide intrinsic notions of
information in the input.
In the standard word-RAM and cell-probe models of computation, we prove that
the optimal query time for dynamic convex hulls is, in fact, 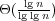 , for
polylogarithmic update time (and word size). Our lower bound is based on a
reduction from the marked-ancestor problem, and is one of the first data structural
lower bounds for a nonorthogonal geometric problem. Our upper bounds
follow a recent trend of attacking nonorthogonal geometric problems from an
information-theoretic perspective that has proved central to advanced data
structures. Interestingly, our upper bounds are the first to successfully apply this
perspective to dynamic geometric data structures, and require substantially different
ideas from previous work. , for
polylogarithmic update time (and word size). Our lower bound is based on a
reduction from the marked-ancestor problem, and is one of the first data structural
lower bounds for a nonorthogonal geometric problem. Our upper bounds
follow a recent trend of attacking nonorthogonal geometric problems from an
information-theoretic perspective that has proved central to advanced data
structures. Interestingly, our upper bounds are the first to successfully apply this
perspective to dynamic geometric data structures, and require substantially different
ideas from previous work.
|
We consider the problem of detecting network faults. Our focus is on
detection schemes that send probes both proactively and non-adaptively.
Such schemes are particularly relevant to all-optical networks, due to these
networks’ operational characteristics and strict performance requirements.
This fault diagnosis problem motivates a new technical framework that we
introduce: group testing with graph-based constraints. Using this framework, we
develop several new probing schemes to detect network faults. The efficiency of
our schemes often depends on the network topology; in many cases we can
show that our schemes are optimal or near-optimal by providing tight lower
bounds.
|
Mihai Pătraşcu
and Mikkel Thorup
18th ACM/SIAM Symposium on Discrete Algorithms ( SODA 2007).
At STOC’06, we presented a new technique for proving cell-probe lower bounds
for static data structures with deterministic queries. This was the first technique
which could prove a bound higher than communication complexity, and it gave the
first separation between data structures with linear and polynomial space. The
new technique was, however, heavily tuned for the deterministic worst-case,
demonstrating long query times only for an exponentially small fraction of the input.
In this paper, we extend the technique to give lower bounds for randomized query
algorithms with constant error probability.
Our main application is the problem of searching predecessors in a static set of n
integers, each contained in a ℓ-bit word. Our trade-off lower bounds are tight
for any combination of parameters. For small space, i.e. n1+o(1), proving
such lower bounds was inherently impossible through known techniques. An
interesting new consequence is that for near linear space, the classic van
Emde Boas search time of O(lg ℓ) cannot be improved, even if we allow
randomization. This is a separation from polynomial space, since Beame and Fich
[STOC’02] give a predecessor search time of O(lg ℓ∕lg lg ℓ) using quadratic
space.
We also show a tight Ω(lg lg n) lower bound for 2-dimensional range queries, via a
new reduction. This holds even in rank space, where no superconstant lower bound
was known, neither randomized nor worst-case. We also slightly improve the best
lower bound for the approximate nearest neighbor problem, when small space is
available.
|
Timothy M. Chan
and Mihai Pătraşcu
SIAM Journal on Computing ( SICOMP), vol. 39(2), 2010. Special issue.
47th IEEE Symposium on Foundations of Computer Science ( FOCS 2006).
Based on two FOCS'06 papers by each author, achieving similar results. My conference paper was entitled: Planar Point Location in Sublogarithmic Time
Given a planar subdivision whose coordinates are integers bounded by U ≤ 2w,
we present a linear-space data structure that can answer point location queries in
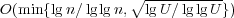 time on the unit-cost RAM with word size w.
This is the first result to beat the standard Θ(lg n) bound for infinite precision
models. time on the unit-cost RAM with word size w.
This is the first result to beat the standard Θ(lg n) bound for infinite precision
models.
As a consequence, we obtain the first o(nlg n) (randomized) algorithms for many
fundamental problems in computational geometry for arbitrary integer input on the
word RAM, including: constructing the convex hull of a three-dimensional point set,
computing the Voronoi diagram or the Euclidean minimum spanning tree of a planar
point set, triangulating a polygon with holes, and finding intersections among a set
of line segments. Higher-dimensional extensions and applications are also
discussed.
Though computational geometry with bounded precision input has been
investigated for a long time, improvements have been limited largely to problems of
an orthogonal flavor. Our results surpass this long-standing limitation, answering, for
example, a question of Willard (SODA’92).
|
Mihai Pătraşcu
and Mikkel Thorup
SIAM Journal on Computing ( SICOMP), vol. 39(2), 2010. Special issue.
47th IEEE Symposium on Foundations of Computer Science ( FOCS 2006).
We convert cell-probe lower bounds for polynomial space into stronger lower
bounds for near-linear space. Our technique applies to any lower bound proved
through the richness method. For example, it applies to partial match, and to
near-neighbor problems, either for randomized exact search, or for deterministic
approximate search (which are thought to exhibit the curse of dimensionality). These
problems are motivated by search in large data bases, so near-linear space is the most
relevant regime.
Typically, richness has been used to imply Ω(d∕lg n) lower bounds for
polynomial-space data structures, where d is the number of bits of a query. This is
the highest lower bound provable through the classic reduction to communication
complexity. However, for space nlg O(1)n, we now obtain bounds of Ω(d∕lg d). This is
a significant improvement for natural values of d, such as lg O(1)n. In the most
important case of d = Θ(lg n), we have the first superconstant lower bound. From a
complexity theoretic perspective, our lower bounds are the highest known
for any static data structure problem, significantly improving on previous
records.
|
We investigate the optimality of (1 + ε)-approximation algorithms obtained via
the dimensionality reduction method. We show that:
- Any data structure for the (1 + ε)-approximate nearest neighbor problem
in Hamming space, which uses constant number of probes to answer each
query, must use
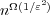 space. space.
- Any algorithm for the (1+ε)-approximate closest substring problem must
run in time exponential in 1∕ε2-γ for any γ > 0 (unless 3SAT can be
solved in sub-exponential time)
Both lower bounds are (essentially) tight.
|
We consider deterministic dictionaries in the parallel disk model, motivated by
applications such as file systems. Our main results show that if the number of disks is
moderately large (at least logarithmic in the size of the universe from which keys
come), performance similar to the expected performance of randomized dictionaries
can be achieved. Thus, we may avoid randomization by extending parallelism. We
give several algorithms with different performance trade-offs. One of our main tools is
a deterministic load balancing scheme based on expander graphs, that may be of
independent interest.
Our algorithms assume access to certain expander graphs “for free”. While
current explicit constructions of expander graphs have suboptimal parameters, we
show how to get near-optimal expanders for the case where the amount of data is
polynomially related to the size of internal memory.
|
We develop a new technique for proving cell-probe lower bounds for static data
structures. Previous lower bounds used a reduction to communication games, which
was known not to be tight by counting arguments. We give the first lower bound for
an explicit problem which breaks this communication complexity barrier. In
addition, our bounds give the first separation between polynomial and near
linear space. Such a separation is inherently impossible by communication
complexity.
Using our lower bound technique and new upper bound constructions, we obtain
tight bounds for searching predecessors among a static set of integers. Given a set Y
of n integers of ℓ bits each, the goal is to efficiently find predecessor(x) =
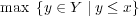 . For this purpose, we represent Y on a RAM with word
length w using S ≥ nℓ bits of space. Defining . For this purpose, we represent Y on a RAM with word
length w using S ≥ nℓ bits of space. Defining 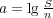 , we show that the optimal
search time is, up to constant factors: , we show that the optimal
search time is, up to constant factors:
In external memory (w > ℓ), it follows that the optimal strategy is to use either
standard B-trees, or a RAM algorithm ignoring the larger block size. In the
important case of w = ℓ = γ lg n, for γ > 1 (i.e. polynomial universes), and near
linear space (such as S = n ⋅ lg O(1)n), the optimal search time is Θ(lg ℓ). Thus,
our lower bound implies the surprising conclusion that van Emde Boas’
classic data structure from [FOCS’75] is optimal in this case. Note that for
space 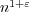 , a running time of O(lg ℓ∕lg lg ℓ) was given by Beame and Fich
[STOC’99]. , a running time of O(lg ℓ∕lg lg ℓ) was given by Beame and Fich
[STOC’99].
|
We develop dynamic dictionaries on the word RAM that use asymptotically
optimal space, up to constant factors, subject to insertions and deletions, and subject
to supporting perfect-hashing queries and/or membership queries, each operation in
constant time with high probability. When supporting only membership queries, we
attain the optimal space bound of 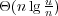 bits, where n and u are the sizes of the
dictionary and the universe, respectively. Previous dictionaries either did not achieve
this space bound or had time bounds that were only expected and amortized. When
supporting perfect-hashing queries, the optimal space bound depends on the
range {1,2,…,n + t} of hashcodes allowed as output. We prove that the
optimal space bound is bits, where n and u are the sizes of the
dictionary and the universe, respectively. Previous dictionaries either did not achieve
this space bound or had time bounds that were only expected and amortized. When
supporting perfect-hashing queries, the optimal space bound depends on the
range {1,2,…,n + t} of hashcodes allowed as output. We prove that the
optimal space bound is 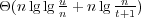 bits when supporting only
perfect-hashing queries, and it is bits when supporting only
perfect-hashing queries, and it is 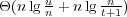 bits when also supporting
membership queries. All upper bounds are new, as is the bits when also supporting
membership queries. All upper bounds are new, as is the 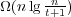 lower
bound. lower
bound.
|
We prove nearly tight lower bounds on the number of rounds of communication
required by efficient protocols over asymmetric channels between a server (with high
sending capacity) and one or more clients (with low sending capacity). This scenario
captures the common asymmetric communication bandwidth between broadband
Internet providers and home users, as well as sensor networks where sensors (clients)
have limited capacity because of the high power requirements for long-range
transmissions. An efficient protocol in this setting communicates n bits from each of
the k clients to the server, where the clients’ bits are sampled from a joint
distribution D that is known to the server but not the clients, with the
clients sending only O(H(D) + k) bits total, where H(D) is the entropy of
distribution D.
In the single-client case, there are efficient protocols using O(1) rounds in
expectation and O(lg n) rounds in the worst case. We prove that this is essentially
best possible: with probability 1∕2O(t lg t), any efficient protocol can be forced to use t
rounds.
In the multi-client case, there are efficient protocols using O(lg k) rounds in
expectation. We prove that this is essentially best possible: with probability Ω(1),
any efficient protocol can be forced to use Ω(lg k∕lg lg k) rounds.
Along the way, we develop new techniques of independent interest for proving
lower bounds in communication complexity.
|
Ilya Baran,
Erik Demaine,
and Mihai Pătraşcu
Algorithmica, vol. 50(4), 2008. Special issue.
9th Workshop on Algorithms and Data Structures ( WADS 2005).
|
Mihai Pătraşcu
and Corina Tarniţă
Theoretical Computer Science ( TCS), vol. 380, 2007. Special issue.
32nd International Colloquium on Automata, Languages and Programming ( ICALP 2005).
Best Student Paper Award (Track A).
|
We consider the problem of maintaining a dynamic set of integers and answering
queries of the form: report a point (equivalently, all points) in a given interval. Range
searching is a natural and fundamental variant of integer search, and can be solved
using predecessor search. However, for a RAM with w-bit words, we show how to
perform updates in O(lg w) time and answer queries in O(lg lg w) time. The update
time is identical to the van Emde Boas structure, but the query time is
exponentially faster. Existing lower bounds show that achieving our query
time for predecessor search requires doubly-exponentially slower updates.
We present some arguments supporting the conjecture that our solution is
optimal.
Our solution is based on a new and interesting recursion idea which is “more
extreme” that the van Emde Boas recursion. Whereas van Emde Boas uses a simple
recursion (repeated halving) on each path in a trie, we use a nontrivial, van Emde
Boas-like recursion on every such path. Despite this, our algorithm is quite clean
when seen from the right angle. To achieve linear space for our data structure,
we solve a problem which is of independent interest. We develop the first
scheme for dynamic perfect hashing requiring sublinear space. This gives a
dynamic Bloomier filter (a storage scheme for sparse vectors) which uses low
space. We strengthen previous lower bounds to show that these results are
optimal.
|
Erik Demaine,
Dion Harmon,
John Iacono,
and Mihai Pătraşcu
SIAM Journal on Computing ( SICOMP), vol. 37(1), 2007. Special issue.
45th IEEE Symposium on Foundations of Computer Science ( FOCS 2004).
We present an O(lg lg n)-competitive online binary search tree, improving upon
the best previous (trivial) competitive ratio of O(lg n). This is the first major
progress on Sleator and Tarjan’s dynamic optimality conjecture of 1985 that
O(1)-competitive binary search trees exist.
|
Stelian Ciurea,
Erik Demaine,
Corina Tarniţă,
and Mihai Pătraşcu
3rd International Conference on Fun with Algorithms ( FUN 2004).
The divisible-pair problem was also covered in a poster at ANTS'04, and an invited abstract in ACM SIGSAM Bulletin, vol. 38(3), 2004. A follow-up paper of Adrian Dumitrescu and Guangwu Xu corrects an error in our divisible-pair upper bound.
We consider two algorithmic problems arising in the lives of Yogi Bear and
Ranger Smith. The first problem is the natural algorithmic version of a classic
mathematical result: any (n + 1)-subset of {1,…,2n} contains a pair of divisible
numbers. How do we actually find such a pair? If the subset is given in the form of
a bit vector, we give a RAM algorithm with an optimal running time of
O(n∕lg n). If the subset is accessible only through a membership oracle, we
show a lower bound of 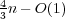 and an almost matching upper bound
of and an almost matching upper bound
of 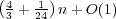 on the number of queries necessary in the worst
case. on the number of queries necessary in the worst
case.
The second problem we study is a geometric optimization problem where the
objective amusingly influences the constraints. Suppose you want to surround n trees
at given coordinates by a wooden fence. However, you have no external wood supply,
and must obtain wood by chopping down some of the trees. The goal is to cut down a
minimum number of trees that can be built into a fence that surrounds the
remaining trees. We obtain efficient polynomial-time algorithms for this
problem.
We also describe an unusual data-structural view of the Nim game, leading to an
intriguing open problem.
|
Corina Tarniţă
and Mihai Pătraşcu
6th Algorithmic Number Theory Symposium ( ANTS 2004).
This is superseded by [25].
We study the problem of computing the k-th term of the Farey sequence of order
n, for given n and k. Several methods for generating the entire Farey sequence are
known. However, these algorithms require at least quadratic time, since the Farey
sequence has Θ(n2) elements. For the problem of finding the k-th element, we obtain
an algorithm that runs in time O(nlg n) and uses space 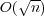 . The same bounds
hold for the problem of determining the rank in the Farey sequence of a given
fraction. A more complicated solution can reduce the space to O(n1∕3(lg lg n)2∕3),
and, for the problem of determining the rank of a fraction, reduce the time to
O(n). We also argue that an algorithm with running time O(polylogn) is
unlikely to exist, since that would give a polynomial-time algorithm for integer
factorization. . The same bounds
hold for the problem of determining the rank in the Farey sequence of a given
fraction. A more complicated solution can reduce the space to O(n1∕3(lg lg n)2∕3),
and, for the problem of determining the rank of a fraction, reduce the time to
O(n). We also argue that an algorithm with running time O(polylogn) is
unlikely to exist, since that would give a polynomial-time algorithm for integer
factorization.
|
Mihai Pătraşcu
and Erik Demaine
SIAM Journal on Computing ( SICOMP), vol. 35(4), 2006. Special issue
36th ACM Symposium on Theory of Computing ( STOC 2004).
This chapter of my PhD thesis contains a better exposition. The conference title was: Lower Bounds for Dynamic Connectivity.
We develop a new technique for proving cell-probe lower bounds on dynamic data
structures. This technique enables us to prove an amortized randomized
Ω(lg n) lower bound per operation for several data structural problems on
n elements, including partial sums, dynamic connectivity among disjoint
paths (or a forest or a graph), and several other dynamic graph problems
(by simple reductions). Such a lower bound breaks a long-standing barrier
of Ω(lg n∕lg lg n) for any dynamic language membership problem. It also
establishes the optimality of several existing data structures, such as Sleator and
Tarjan’s dynamic trees. We also prove the first Ω(log Bn) lower bound in the
external-memory model without assumptions on the data structure (such as the
comparison model). Our lower bounds also give a query-update trade-off curve
matched, e.g., by several data structures for dynamic connectivity in graphs.
We also prove matching upper and lower bounds for partial sums when
parameterized by the word size and the maximum additive change in an
update.
|
Erik Demaine,
Thouis Jones,
and Mihai Pătraşcu
15th ACM/SIAM Symposium on Discrete Algorithms ( SODA 2004).
Errata: There is an error in Lemma 2.1, regarding the behavior on the uniform distribution. The behavior as stated is correct, but the justification is not.
We define a deterministic metric of “well-behaved data” that enables searching
along the lines of interpolation search. Specifically, define Δ to be the ratio of
distances between the farthest and nearest pair of adjacent elements. We develop a
data structure that stores a dynamic set of n integers subject to insertions, deletions,
and predecessor/successor queries in O(lg Δ) time per operation. This result
generalizes interpolation search and interpolation search trees smoothly to
nonrandom (in particular, non-independent) input data. In this sense, we
capture the amount of “pseudorandomness” required for effective interpolation
search.
|
Mihai Pătraşcu
and Erik Demaine
15th ACM/SIAM Symposium on Discrete Algorithms ( SODA 2004).
Invited to special issue of ACM Transactions on Algorithms (declined). Merged with [3] for the journal version.
We close the gaps between known lower and upper bounds for the online
partial-sums problem in the RAM and group models of computation. If elements
are chosen from an abstract group, we prove an Ω(lg n) lower bound on
the number of algebraic operations that must be performed, matching a
well-known upper bound. In the RAM model with b-bit memory registers,
we consider the well-studied case when the elements of the array can be
changed additively by δ-bit integers. We give a RAM algorithm that achieves
a running time of Θ(1 + lg n∕lg(b∕δ)) and prove a matching lower bound
in the cell-probe model. Our lower bound is for the amortized complexity,
and makes minimal assumptions about the relations between n, b, and δ.
The best previous lower bound was Ω(lg n∕(lg lg n + lg b)), and the best
previous upper bound matched only in the special case b = Θ(lg n) and
δ = O(lg lg n).
| |